
【题目】如图,梯形ABCD中,AD∥BC,AB=DC,点P是AD边上一点,联结PB、PC,且AB2=APPD,则图中有对相似三角形. 
【答案】3
【解析】解:∵AD∥BC,AB=DC, ∴梯形ABCD为等腰梯形,
∴∠A=∠D,
∵AB2=APPD,
∴ABCD=APPD,即 ![]() =
= ![]() ,
,
∴△ABP∽△DPC,
∴∠ABP=∠DPC,
∵AD∥BC,
∴∠DPC=∠PCB,∠APB=∠PBC,
∴∠PCB=∠ABP,
∴△ABP∽△PCB,
∴△DPC∽△DPC.
所以答案是3.
【考点精析】根据题目的已知条件,利用相似三角形的判定的相关知识可以得到问题的答案,需要掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).


科目:初中数学 来源: 题型:
【题目】甲、乙两人都从A出发经B地去C地,乙比甲晚出发1分钟,两人同时到达B地,甲在B地停留1分钟,乙在B地停留2分钟,他们行走的路程y(米)与甲行走的时间x(分钟)之间的函数关系如图所示,则下列说法中正确的个数有( ) ①甲到B地前的速度为100m/min
②乙从B地出发后的速度为300m/min
③A、C两地间的路程为1000m
④甲乙再次相遇时距离C地300km.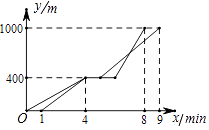
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学九年级学生中考体育成绩情况,现从中抽取部分学生的体育成绩进行分段(A:50分、B:49~40分、C:39~30分、D:29~0分)统计,统计结果如图所示. 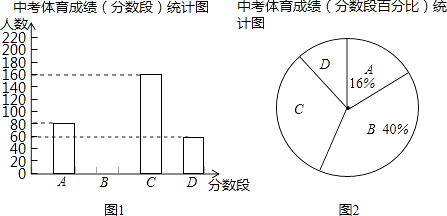
根据上面提供的信息,回答下列问题:
(1)本次抽查了多少名学生的体育成绩;
(2)补全图9.1,求图9.2中D分数段所占的百分比;
(3)已知该校九年级共有900名学生,请估计该校九年级学生体育成绩达到40分以上(含40分)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】x1 , x2是关于x的一元二次方程x2﹣mx+m﹣2=0的两个实数根,是否存在实数m使 ![]() +
+ ![]() =0成立?则正确的结论是( )
=0成立?则正确的结论是( )
A.m=0时成立
B.m=2时成立
C.m=0或2时成立
D.不存在
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给定直线l:y=kx,抛物线C:y=ax2+bx+1.
(1)当b=1时,l与C相交于A,B两点,其中A为C的顶点,B与A关于原点对称,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线l′,则无论非零实数k取何值,直线l′与抛物线C都只有一个交点.
①求此抛物线的解析式;
②若P是此抛物线上任一点,过P作PQ∥y轴且与直线y=2交于Q点,O为原点.求证:OP=PQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+kx+k﹣1图象过点A和点C,抛物线与x轴的另一交点是B,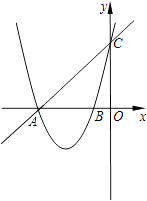
(1)求出此抛物线的解析式、对称轴以及B点坐标;
(2)若在y轴负半轴上存在点D,能使得以A、C、D为顶点的三角形与△ABC相似,请求出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D在边AB上,线段DC绕点D逆时针旋转,端点C恰巧落在边AC上的点E处.如果 ![]() =m,
=m, ![]() =n.那么m与n满足的关系式是:m=(用含n的代数式表示m).
=n.那么m与n满足的关系式是:m=(用含n的代数式表示m). 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com