
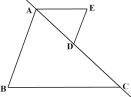
【题目】如图1,AB,BC被直线AC所截,点D是线段AC上的点,过点D作DE//AB,连接AE,∠B=∠E=70°.
(1)请说明AE//BC的理由.
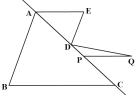
(2)将线段AE沿着直线AC平移得到线段PQ,连接DQ.
①如图2,当DE⊥DQ时,求∠Q的度数;
②在整个运动中,当∠Q=2∠EDQ时,则∠Q= .
【答案】(1)详见解析;(2)①20°;②![]()
【解析】
(1)由DE//AB,可得∠BAE+∠E=180°,从而可证∠BAE+∠B=180°,根据从旁内角互补,两直线平行可证AB//DE;
(2)①过D点作DF//AE,由平行线的性质可得∠EDF=70°,由DE⊥DQ,可得∠FDQ=20°,进而可的求出∠Q=20°;②如图,作DF//AE,根据平行线的性质解答即可.
(1)证明:∵DE//AB,
∴∠BAE+∠E=180°.
又∵∠B=∠E,
∴∠BAE+∠B=180°,
∴AB//DE;
(2)①过D点作DF//AE,
∵PQ//AE ,
∴DF//PQ,
∵∠E=70°,
∴∠EDF=70°.
∵DE⊥DQ,
∴∠EDQ=90°,
∴∠FDQ=90°-70°=20°,
∴∠Q=∠FDQ=20°;
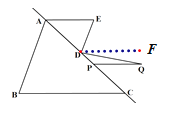
②如图,作DF//AE,
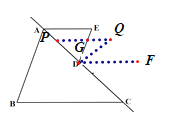
∵PQ//AE ,
∴DF//PQ,
∴∠Q=∠QDF,∠E=∠EDF=70°,
∴∠EDQ+∠Q=70°,
∵∠Q=2∠EDQ,
∴![]() ∠Q+∠Q=70°,
∠Q+∠Q=70°,
∴∠Q=(![]() )°.
)°.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】如图,P为正方形ABCD对角线AC上一动点,EF⊥AC且交AD于E,交CD的延长线于点G,连接CE和AG.
(1)求证:△ADG≌△CDE;
(2)当CE平分∠ACD时,求tan∠AGD.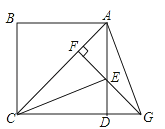
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知A(0,-2),B(-2,1),C(3,2)
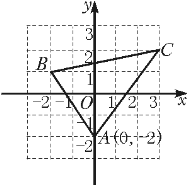
(1)求线段AB、BC、AC的长;
(2)把A、B、C三点的横坐标、纵坐标都乘以2,得到A′、B′、C′的坐标,求A′B′、B′C′、A′C′的长;
(3)以上六条线段成比例吗?
(4)△ABC与△A′B′C′的形状相同吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校七年级学生参加“数学素养水平测试”的成绩情况,在全段学生中抽查一部分学生的成绩,整理后按A、B、C、D四个等级绘制成如下两幅统计图(部分项目不完整).
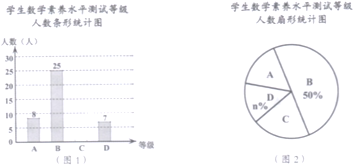
(1)根据统计图所提供的信息,得出抽查学生共有 人,图2中![]() .
.
(2)补全条形统计图1,图2中等级C所对应的扇形的圆心角度数为 .
(3)该校共有800名七年级学生参加素养水平测试,请估算等级A的学生人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分)的变化示意图:
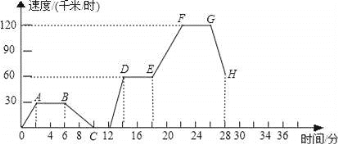
(1)从点A到点B、点E到点F、点G到点H分别表明汽车在什么状态?
(2)分段描述汽车在第0分种到第28分钟的行驶情况;
(3)汽车在点A的速度是多少?在点C呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
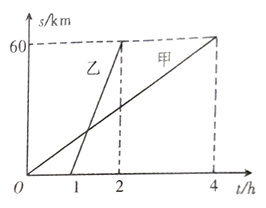
【题目】![]() 两地相距
两地相距![]() ,甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由
,甲、乙二人分别骑自行车和摩托车沿相同路线匀速行驶,由![]() 地到达
地到达![]() 地.他们行驶的路程
地.他们行驶的路程![]() 与甲出发后的时间
与甲出发后的时间![]() 之间的函数图像如图所示.
之间的函数图像如图所示.
(1)乙比甲晚出发几小时?乙比甲早到几小时?
(2)分别写出甲、乙行驶的路程![]() 与甲出发后的时间
与甲出发后的时间![]() 的函数关系式(不写自变量的取值范围).
的函数关系式(不写自变量的取值范围).
(3)乙在甲出发后几小时追上甲?追上甲的地点离![]() 地有多远?
地有多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com