

���� ��1���������E�ĺ����꣬����ֱ��DE�Ľ���ʽ���E�������꣬��C��0��4����P�ĺ�����Ϊ2�����ݶ������깫ʽ���b��ֵ���ѵ�C��������������ߵĽ���ʽ�п����c��ֵ��д�������ߵĽ���ʽ��
��2�������κ����Ľ���ʽ�䷽�ö���P������Ϊ��2��$\frac{16}{3}$��������ֱ��PC�Ľ���ʽ������PC��QO���õ�ֱ��OQ�Ľ���ʽΪ��y=-$\frac{3}{2}$x������ΪQ��PH�ϣ���Q�ĺ�����Ϊ2���Ӷ�������Q�������ꣻ
��3���������ߣ�����ֱ�������κ�ȫ�������Σ������÷��������B�����꣬��OB=6��֤����ECD�ա�EMB���á�DEB�ǵ���ֱ�������Σ���֤��DNG�ס�BOD����$\frac{DN}{BO}=\frac{NG}{OD}$���з������a��ֵ��д����G������Ϊ��1��5�������ݽ���ʽ�з����������F�����꣬�����������빫ʽ��FG�ij����õ�QR�ij������ù��ɶ�����RS�ij��������������OR�ij���
���  �⣺��1����ͼ1���ߵ�E��C����ֱ��PH�Գƣ�
�⣺��1����ͼ1���ߵ�E��C����ֱ��PH�Գƣ�
��CE��PH��
��PH�������ߵĶԳ��ᣬ��CE=4��
���E�ĺ�����Ϊ4��
��x=4ʱ��y=$\frac{1}{2}$��4+2=4��
��x=0ʱ��y=2��
��E��4��4����D��0��2����C��0��4����
��C��0��4������y=-$\frac{1}{3}$x2+bx+c�ã�c=4��
���P�ĺ�����Ϊ2��
��-$\frac{b}{2����-\frac{1}{3}��}$=2��
b=$\frac{4}{3}$��
�������ߵĽ���ʽΪ��y=-$\frac{1}{3}$x2+$\frac{4}{3}$x+4��
��2����ͼ2��y=-$\frac{1}{3}$x2+$\frac{4}{3}$x+4=-$\frac{1}{3}$��x-2��2+$\frac{16}{3}$��
��P��2��$\frac{16}{3}$����
��ֱ��PC�Ľ���ʽΪ��y=kx+b��
��P��2��$\frac{16}{3}$����C��0��4������ã�$\left\{\begin{array}{l}{2k+b=\frac{16}{3}}\\{b=4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=4}\end{array}\right.$��
��ֱ��PC�Ľ���ʽΪ��y=$\frac{2}{3}$x+4��
��PC��QO��
��ֱ��OQ�Ľ���ʽΪ��y=-$\frac{3}{2}$x��
��Q��PH�ϣ�
��Q�ĺ�����Ϊ2��
��x=2ʱ��y=-$\frac{3}{2}$��2=-3��
��Q��2��-3����
��Q��������Ϊ-3��
��3����ͼ3����G��GN��y����N����E��EM��x����M����Q��QS��y����S������EB��GD��
��G��a��-$\frac{1}{3}{a}^{2}$+$\frac{4}{3}$a+4����
��y=0ʱ��-$\frac{1}{3}$x2+$\frac{4}{3}$x+4=0��
��ã�x1=-2��x2=6��
��OB=6��
��E��4��4����
��EC=EM=4��
��BM=6-4=2��
��CD=OC-OD=4-2=2��
��BM=CD��
�ߡ�ECD=��EMB=90�㣬
���ECD�ա�EMB��
���DEC=��BEM��DE=BE��
�ߡ�ECO=��COB=��EMO=90�㣬
���ı���COME�Ǿ��Σ�
���CEM=90�㣬
���CED+��DEM=90�㣬
���DEM+��BEM=90�㣬
���DEB=90�㣬
���DEB�ǵ���ֱ�������Σ�
���EDB=45�㣬
��GF��DF��GE=FE��
��GK=KF��
��Rt��DKF�У���EDF=45�㣬
���DKFҲ�ǵ���ֱ�������Σ�
��DK=KF��
��DK=GK��
���DKG�ǵ���ֱ�������Σ�
���GDE=45�㣬
���GDF=90�㣬
���NDG+��ODB=90�㣬
�ߡ�ODB+��DBO=90�㣬
���NDG=��DBO��
�ߡ�DNG=��DOB=90�㣬
���DNG�ס�BOD��
��$\frac{DN}{BO}=\frac{NG}{OD}$��
��DN•OD=BO•NG��
��2��-$\frac{1}{3}{a}^{2}$+$\frac{4}{3}$a+4-2��=6a��
��ã�a1=-6���ᣩ��a2=1��
��a=1ʱ��y=-$\frac{1}{3}{a}^{2}$+$\frac{4}{3}$a+4=-$\frac{1}{3}$+$\frac{4}{3}$+4=5��
��G��1��5����
��ֱ��ED�Ľ���ʽΪ��y=$\frac{1}{2}$x+2����ED��FG��
����FG�Ľ���ʽΪ��y=-2x+b��
��G��1��5������ã�-2+b=5��
b=7��
��FG�Ľ���ʽΪ��y=-2x+7��
��ֱ��BD�Ľ���ʽΪ��y=kx+b��
��B��6��0����D��0��2������ã�$\left\{\begin{array}{l}{6k+b=0}\\{b=2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=2}\end{array}\right.$��
��ֱ��BD�Ľ���ʽΪ��y=-$\frac{1}{3}$x+2��
����$\left\{\begin{array}{l}{y=-\frac{1}{3}x+2}\\{y=-2x+7}\end{array}\right.$ ��ã�$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$��
��F��3��1����
��FG=$\sqrt{��3-1��^{2}+��1-5��^{2}}$=2$\sqrt{5}$��
��FG=2QR��
��QR=$\sqrt{5}$��
��Q��2��-3����
��QS=2��OS=3��
�ɹ��ɶ����ã�RS=$\sqrt{��\sqrt{5}��^{2}-{2}^{2}}$=1��
������������ٵ�R��S���Ϸ�ʱ��OR=OS-RS=3-1=2��
�ڵ�R��S���·�ʱ��OR=OS+RS=3+1=4��
���߶�OR�ij�Ϊ2��4��
���� �����Ƕ��κ������ۺ��⣬���������ô���ϵ������һ�κ����Ľ���ʽ�������ý���ʽ��ʾ������꣬���ݵ�����ϵʽ��һԪ���η��������ĸ��ֵ��д��������ꣻ�����������̡�ͼ���л��ؽ�ϣ��Ƚϸ��ӣ��ڼ�������У���������ֱ���ഹֱ����һ����ϵ��kΪ�������������������빫ʽ���ɶ������߶εij�����ֱ�ߵĽ���ʽ�з��������佻�����ꣻ����ȫ�Ⱥ����Ƶ����ʵõ��ߵĹ�ϵ���Ӷ��ó����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ��ֱ������ϵ�У���PΪ��-2��3�����Ե�OΪԲ�ģ���OP�ij�Ϊ�뾶��������x��ĸ������ڵ�A�����A�ĺ�������ڣ�������
��ͼ����ƽ��ֱ������ϵ�У���PΪ��-2��3�����Ե�OΪԲ�ģ���OP�ij�Ϊ�뾶��������x��ĸ������ڵ�A�����A�ĺ�������ڣ�������| A�� | -2.5��-3֮�� | B�� | -3��-3.5֮�� | C�� | -3.5��-4֮�� | D�� | -4��-4.5 ֮�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m3•m2=m6 | B�� | ��xy��8�£�xy��4=��xy��2 | ||
| C�� | a10�£�a7��a2��=a5 | D�� | x4m+x2n•x2n=1��nΪ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+y | B�� | xy | C�� | 10+y | D�� | 10xy |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
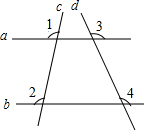 ��ͼ��ֱ��a��b��ֱ��c��d�ཻ����֪��1=��2����3=110�㣬���4�Ķ���Ϊ110�㣮
��ͼ��ֱ��a��b��ֱ��c��d�ཻ����֪��1=��2����3=110�㣬���4�Ķ���Ϊ110�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB�ǡ�O��ֱ����AB=4$\sqrt{3}$����C��OA���е㣬����C��CD��AB����O��D�㣬��E�ǡ�O��һ�㣬����DE��AE��DC���ӳ����ڵ�F����AE•AF��ֵΪ12��
��ͼ��AB�ǡ�O��ֱ����AB=4$\sqrt{3}$����C��OA���е㣬����C��CD��AB����O��D�㣬��E�ǡ�O��һ�㣬����DE��AE��DC���ӳ����ڵ�F����AE•AF��ֵΪ12���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���߶�AB�ij�Ϊ5��CΪ�߶�AB��һ���㣨���A��B���غϣ����ֱ���AC��BCΪб����AB��ͬ��������ֱ��������ACD��BCE����AD=x��BE=y����ôx2+y2��Сֵ��$\frac{25}{4}$��
��ͼ���߶�AB�ij�Ϊ5��CΪ�߶�AB��һ���㣨���A��B���غϣ����ֱ���AC��BCΪб����AB��ͬ��������ֱ��������ACD��BCE����AD=x��BE=y����ôx2+y2��Сֵ��$\frac{25}{4}$���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com