
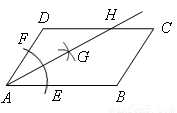
如图,在平行四边形ABCD中,AB>CD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于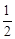 EF的长半径画弧,两弧交于点G;作射线AG交CD于点H。则下列结论:
EF的长半径画弧,两弧交于点G;作射线AG交CD于点H。则下列结论:
①AG平分∠DAB,②CH=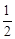 DH,③△ADH是等腰三角形,④S△ADH=
DH,③△ADH是等腰三角形,④S△ADH=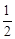 S四边形ABCH。
S四边形ABCH。
其中正确的有
A.①②③ B.①③④ C.②④ D.①③
D
【解析】
试题分析:①如图,连接EG,FG,

由作图可得,AE=AF,EG=FG,
又∵AG=AG,∴△AEG≌△AFG(SSS)。
∴∠EAG=∠FAG,即AG平分∠DAB。故结论①正确。
③∵在平行四边形ABCD中,DC∥AB,∴∠HAB=DHA。
由①∠HAB=∠HAD,∴∠HAD=DHA。∴DA=DH,即△ADH是等腰三角形。故结论③正确。
②若CH= DH,由③可得AB=DC=
DH,由③可得AB=DC= AD,与已知AB>CD条件不符。故结论②错误。
AD,与已知AB>CD条件不符。故结论②错误。
④若S△ADH= S四边形ABCH,由③可得AB=DC=
S四边形ABCH,由③可得AB=DC= AD,与已知AB>CD条件不符。故结论②错误。
AD,与已知AB>CD条件不符。故结论②错误。
综上所述,正确的有①③。故选D。


科目:初中数学 来源: 题型:
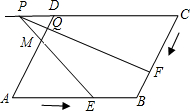 的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.
的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.查看答案和解析>>
科目:初中数学 来源: 题型:
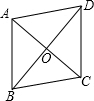 如图,在平行四边形ABCD中,AB=2
如图,在平行四边形ABCD中,AB=2| 2 |
| 3 |
| 5 |
| A、AC⊥BD |
| B、四边形ABCD是菱形 |
| C、△ABO≌△CBO |
| D、AC=BD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com