
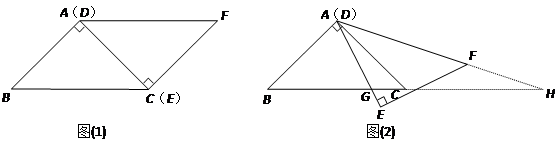
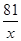 (9
(9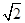 ≥x>0),
≥x>0),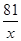 (9
(9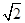 ≥x>0).
≥x>0).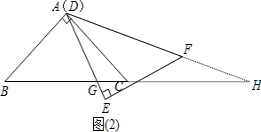
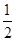 BC时,∠GAC=∠H<∠HAG,
BC时,∠GAC=∠H<∠HAG,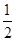 BC时,G为BC的中点,H与C重合,△AGH是等腰三角形,
BC时,G为BC的中点,H与C重合,△AGH是等腰三角形,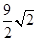 ,即x=
,即x=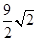 ,
,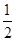 BC时,由(1)△AGC∽△HGA,
BC时,由(1)△AGC∽△HGA,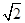 .
.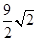 或9
或9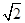 时,△AGH是等腰三角形.
时,△AGH是等腰三角形.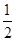 BC时,当CG=
BC时,当CG=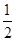 BC时,当CG>
BC时,当CG> BC时分别得出即可.
BC时分别得出即可.

科目:初中数学 来源:不详 题型:单选题
| A.△ADE∽△AEF | B.△ADE∽△ECF | C.△ECF∽△AEF | D.△AEF∽△ABF |
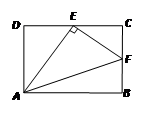
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
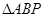 ∽
∽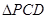 ,从而得到
,从而得到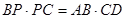 ,解答下列问题.
,解答下列问题.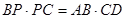 仍成立吗? 试说明理由;
仍成立吗? 试说明理由;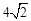 ,AF=3,求FG的长.
,AF=3,求FG的长.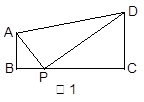
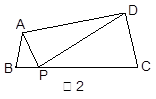
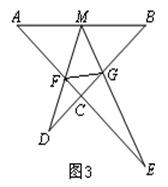
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
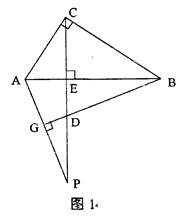
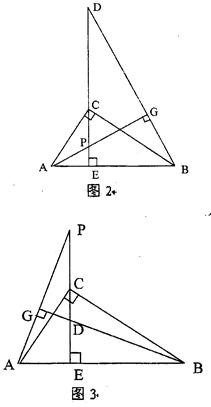
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
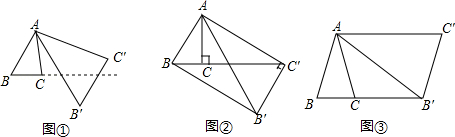
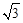 ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.20米 | B.18米 | C.16米 | D.15米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com