
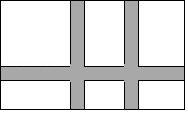
 如图所示,要在20米宽,32米长的矩形耕地上修筑同样宽的三条小路(两条纵向,一条横向,横向与纵向互相垂直),把耕地分成大小不等的六块花田.
如图所示,要在20米宽,32米长的矩形耕地上修筑同样宽的三条小路(两条纵向,一条横向,横向与纵向互相垂直),把耕地分成大小不等的六块花田.分析 (1)本题中,试验地的面积=矩形耕地的面积-三条道路的面积+道路重叠部分的两个小正方形的面积.如果设道路宽x,可根据此关系列出方程求出x的值,然后将不合题意的舍去即可.
(2)设这个增长率是x,根据花田总收入为50万元,预计2016总收入达到72万元,列出方程,求解即可.
解答 解:(1)设道路为x米宽,
由题意得:20×32-20x×2-32x+2x2=570,
整理得:x2-36x+35=0,
解得:x=1,x=35,
经检验是原方程的解,但是x=35>20,因此不合题意舍去.
答:道路为1m宽.
(2)设这个增长率是x,
依题意得:50(1+x)2=72,
解得x1=0.2=20%,x2=-2.2(舍去).
答:这个增长率是20%.
点评 此题考查了一元二次方程的应用,掌握增长率问题是本题的关键,若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -6和-$\frac{1}{6}$ | B. | 6x2y和$\frac{2y{x}^{2}}{3}$ | C. | $\frac{1}{2}$a2b和-$\frac{1}{2}$ab2 | D. | 3m2n和-πm2n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com