
【题目】如图,在矩形ABCD中,AB=6,AD=11.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边始终经过点C,另一直角边与AB交于点E. 请问:△CDP与△PAE相似吗?如果相似,请写出证明过程.
【答案】解:△CDP∽△PAE.理由如下: ∵四边形ABCD是矩形,
∴∠D=∠A=90°,CD=AB=6,
∴∠PCD+∠DPC=90°,
又∵∠CPE=90°,
∴∠EPA+∠DPC=90°,
∴∠PCD=∠EPA,
∴△CDP∽△PAE.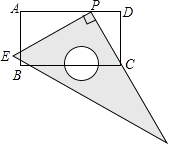
【解析】根据矩形的性质,推出∠D=∠A=90°,再由直角三角形的性质,得出∠PCD+∠DPC=90°,又因∠CPE=90°,推出∠EPA+∠DPC=90°,∠PCD=∠EPA,从而证明△CDP∽△PAE.
【考点精析】关于本题考查的相似三角形的判定,需要了解相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS)才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】王浩同学用木板制作一个带有卡槽的三角形手机架,如图1所示.已知AC=20cm,BC=18cm,∠ACB=50°,王浩的手机长度为17cm,宽为8cm,王浩同学能否将手机放入卡槽AB内?请说明你的理由.(提示:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把抛物线y= ![]() x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=
x2平移得到抛物线m,抛物线m经过点A(﹣6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y= ![]() x2交于点Q,则图中阴影部分的面积为 .
x2交于点Q,则图中阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y= ![]() ,当x>0时,y随x的增大而增大,则关于x的方程ax2﹣2x+b=0的根的情况是( )
,当x>0时,y随x的增大而增大,则关于x的方程ax2﹣2x+b=0的根的情况是( )
A.有两个正根
B.有两个负根
C.有一个正根一个负根
D.没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把直角△ABC的斜边AC放在定直线l上,按顺时针的方向在直线l上转动两次,使它转到△A2B1C2的位置,设AB= ![]() ,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )
,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( ) 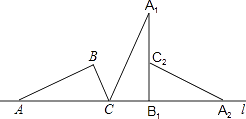
A.( ![]() +
+ ![]() )π
)π
B.( ![]() +
+ ![]() )π
)π
C.2π
D.![]() π
π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知抛物线C1、C2关于x轴对称,抛物线C1 , C3关于y轴对称,如果抛物线C2的解析式是y=﹣ ![]() (x﹣2)2+2,那么抛物线C3的解析式是( )
(x﹣2)2+2,那么抛物线C3的解析式是( ) 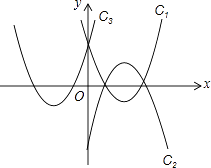
A.y=﹣ ![]() (x﹣2)2﹣2
(x﹣2)2﹣2
B.y=﹣ ![]() (x+2)2+2??
(x+2)2+2??
C.y= ![]() (x﹣2)2﹣2
(x﹣2)2﹣2
D.y= ![]() (x+2)2﹣2
(x+2)2﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《雁栖塔》位于怀柔“北京雁栖湖国际会都中心”所处大岛西南部突出部位的半岛上,是“北京雁栖湖国际会都中心”的标志性建筑,也是整个雁栖湖风景区的标志性建筑. 某校数学课外小组为了测量《雁栖塔》(底部可到达)的高度,准备了如下的测量工具:①平面镜,②皮尺,③长为1米的标杆,④高为1.5m的测角仪(测量仰角、俯角的仪器).第一组选择用②④做测量工具;第二组选用②③做测量工具;第三组利用自身的高度并选用①②做测量工具,分别画出如下三种测量方案示意图.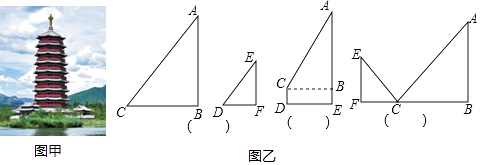
(1)请你判断如下测量方案示意图各是哪个小组的,在测量方案示意图下方的括号内填上小组名称.
(2)选择其中一个测量方案示意图,写出求《雁栖塔》高度的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,过点D作DE⊥AB于点E. 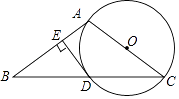
(1)求证:DE是⊙O的切线;
(2)若AC=10,BC=16,求DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com