
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC、AC交于点D、E,过点D作DF⊥AC于点F.
(1)若⊙O的半径为3,∠CDF=15°,求阴影部分的面积;
(2)求证:DF是⊙O的切线;
(3)求证:∠EDF=∠DAC.
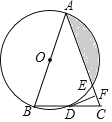
【答案】(1)阴影部分的面积为3π﹣![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】(1)连接OE,过O作OM⊥AC于M,求出AE、OM的长和∠AOE的度数,分别求出△AOE和扇形AOE的面积,即可求出答案;
(2)连接OD,求出OD⊥DF,根据切线的判定求出即可;
(3)连接BE,求出∠FDC=∠EBC,∠FDC=∠EDF,即可求出答案.
详(1)解: 连接OE,过O作OM⊥AC于M,则∠AMO=90°,
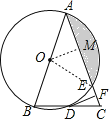
∵DF⊥AC,
∴∠DFC=90°,
∵∠FDC=15°,
∴∠C=180°-90°-15°=75°,
∵AB=AC,
∴∠ABC=∠C=75°,
∴∠BAC=180°-∠ABC∠C=30°,
∴OM=![]() OA=
OA=![]() ×3=
×3=![]() ,AM=
,AM=![]() OM=
OM=![]() ,
,
∵OA=OE,OM⊥AC,
∴AE=2AM=3![]() ,
,
∴∠BAC=∠AEO=30°,
∴∠AOE=180°-30°-30°=120°,
∴阴影部分的面积S=S扇形AOE-S△AOE=![]() ;
;
(2)证明:连接OD,
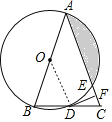
∵AB=AC,OB=OD,
∴∠ABC=∠C,∠ABC=∠ODB,
∴∠ODB=∠C,
∴AC∥OD,
∵DF⊥AC,
∴DF⊥OD,
∵OD过O,
∴DF是⊙O的切线;
(3)证明:连接BE,
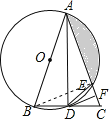
∵AB为⊙O的直径,
∴∠AEB=90°,
∴BE⊥AC,
∵DF⊥AC,
∴BE∥DF,
∴∠FDC=∠EBC,
∵∠EBC=∠DAC,
∴∠FDC=∠DAC,
∵A、B、D、E四点共圆,
∴∠DEF=∠ABC,
∵∠ABC=∠C,
∴∠DEC=∠C,
∵DF⊥AC,
∴∠EDF=∠FDC,
∴∠EDF=∠DAC.


科目:初中数学 来源: 题型:
【题目】现有两个纸箱,每个纸箱内各装有4个材质、大小都相同的乒乓球,其中一个纸箱内4个小球上分别写有1、2、3、4这4个数,另一个纸箱内4个小球上分别写有5、6、7、8这4个数,甲、乙两人商定了一个游戏,规则是:从这两个纸箱中各随机摸出一个小球,然后把两个小球上的数字相乘,若得到的积是2的倍数,则甲得1分,若得到积是3的倍数,则乙得2分.完成一次游戏后,将球分别放回各自的纸箱,摇匀后进行下一次游戏,最后得分高者胜出.。
(1)请你通过列表(或树状图)分别计算乘积是2的倍数和3的倍数的概率;
(2)你认为这个游戏公平吗?为什么?若你认为不公平,请你修改得分规则,使游戏对双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,等腰三角形PEF中,PE=PF,点O在EF边上(异于点E,F),点Q是PO延长线上一点,若△EFQ为等腰三角形,则称点Q为△PEF的“同类点”.
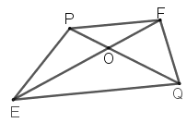
(1)如图,BG平分∠MBN,过射线BM上的点A作AD∥BN,交射线BG于点D,点O为BD上一点,连接AO并延长交射线BN于点C,若∠BAD=100°,∠BCD=70°,求证:点C是△ABD的“同类点”;
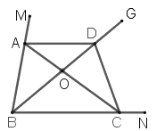
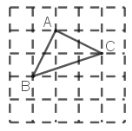
(2)如图③,在5×5的正方形网格图上有一个△ABC,点A,B,C均在格点上,在给出的网格图上有一个格点D,使得点D为△ABC的“同类点”,则这样的点D共有__________个;
(3)凸四边形ABCD中,∠ABC=110°,DA=AB=BC,对角线AC,BD交于点O,且BD≠CD,若点C为△ABD的“同类点”,请直接写出满足条件的∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
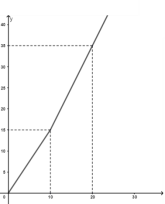
【题目】我国是世界上严重缺水的国家之一。为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费。即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费。设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示。
(1)求a的值;某户居民上月用水8吨,应收水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数关系式;
(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了预测本校九年级男生毕业体育测试达标情况,随机抽取该年级部分男生进行了一次测试(满分50分,成绩均记为整数分),并按测试成绩m(单位:分)分成四类:A类(45<m≤50),B类(40<m≤45),C类(35<m≤40),D类(m≤35)绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
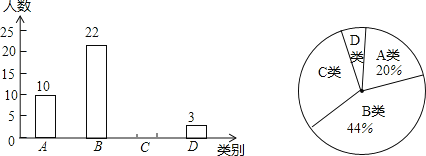
(1)求本次抽取的样本容量和扇形统计图中A类所对的圆心角的度数;
(2)若该校九年级男生有500名,D类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上![]() ,
,![]() 两点对应的有理数分别为
两点对应的有理数分别为![]() 和12,点
和12,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿数轴负方向运动,点
出发,以每秒1个单位长度的速度沿数轴负方向运动,点![]() 同时从点
同时从点![]() 出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为
出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为![]() 秒.
秒.
![]()
(1)求经过2秒后,数轴点![]() 、
、![]() 分别表示的数;
分别表示的数;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)在运动过程中是否存在时间![]() 使
使![]() ,若存在,请求出此时
,若存在,请求出此时![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
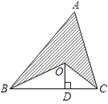
【题目】如图,在△ABC中,AB+AC=20,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则图中阴影部分的面积等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠4﹦180°,∠2﹦∠E,则EF∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.
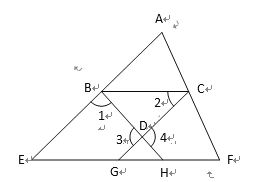
证明:
∵∠1+∠4﹦180°( ),
∠3﹦∠4 ( ),
∴∠1﹢ ﹦180°.
∴AE∥CG ( )
∴∠E﹦∠CGF( ).
∵∠2﹦∠E(已知)
∴ ∠2﹦∠CGF( ).
∴ BC∥EF( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com