
 如图,AD∥BE,BD∥CE.
如图,AD∥BE,BD∥CE.分析 (1)根据平行线成线段成比例得到$\frac{OA}{OB}=\frac{OD}{OE}$,$\frac{OB}{OC}=\frac{OD}{OE}$,等量代换即可得到结论;
(2)根据$\frac{OA}{OB}$=$\frac{OB}{OC}$,代入数据即可得到结论.
解答 (1)证明:∵AD∥BE,
∴$\frac{OA}{OB}=\frac{OD}{OE}$,
∵BD∥CE,
∴$\frac{OB}{OC}=\frac{OD}{OE}$,
∴$\frac{OA}{OB}$=$\frac{OB}{OC}$;
(2)解:∵OA=4,AC=12,
∴OC=16,
∵$\frac{OA}{OB}$=$\frac{OB}{OC}$,
∴$\frac{4}{OB}=\frac{OB}{16}$,
∴OB=8.
点评 本题考查了平行线分线段成比例定理的应用,能根据定理得出比例式是解此题的关键,注意:一组平行线截两条直线,所截得的对应线段成比例.


科目:初中数学 来源: 题型:选择题
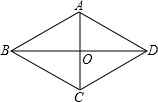 如图,在菱形ABCD中,∠BAD=120°,设∠ABD=α,则下列等式正确的是( )
如图,在菱形ABCD中,∠BAD=120°,设∠ABD=α,则下列等式正确的是( )| A. | sinα=$\frac{\sqrt{3}}{2}$ | B. | tanα=$\sqrt{3}$ | C. | cosα=$\frac{1}{2}$ | D. | cosα=$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
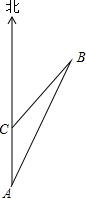 如图.已知一货轮在A处测得灯塔B其北偏东30°方向上,货轮以每小时10海里速度向正北方向航行,1小时后到达C处.并得灯塔B在货轮的北偏东45°方向上.如果货轮不改变方向.请问再过多少小时货轮距灯塔最近?
如图.已知一货轮在A处测得灯塔B其北偏东30°方向上,货轮以每小时10海里速度向正北方向航行,1小时后到达C处.并得灯塔B在货轮的北偏东45°方向上.如果货轮不改变方向.请问再过多少小时货轮距灯塔最近?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
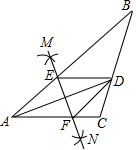 如图,在△ABC中,AD平分∠BAC,按如下步骤作图:
如图,在△ABC中,AD平分∠BAC,按如下步骤作图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com