
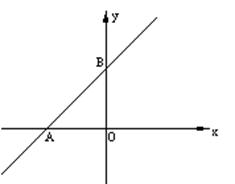
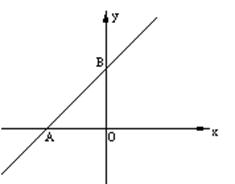
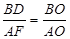 ,
, (yE-yM)=
(yE-yM)= =2
=2

 ( yM-yA)=
( yM-yA)= (a+4),BE=
(a+4),BE= |yE-yB|=
|yE-yB|= |a+2|,
|a+2|, (a+4)= -
(a+4)= - (a+2)
(a+2) (a+4)=
(a+4)=  (a+2)
(a+2)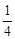 AB=
AB=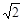
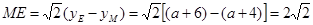 ,
,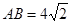 ,所以AB=2ME;
,所以AB=2ME; (
( 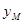 -
- )=
)= (a+4),BE=
(a+4),BE= |
|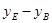 |=
|= |a+2|,AM=BE,结合条件-4<a<0,且a≠2,a=-3,可知M(-3,1);当-2<a<0时,a不存在。
|a+2|,AM=BE,结合条件-4<a<0,且a≠2,a=-3,可知M(-3,1);当-2<a<0时,a不存在。

科目:初中数学 来源:不详 题型:单选题
| A.(-1,-2 ) | B.(1,-2 ) | C.(2,-1 ) | D.(-2,1 ) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
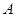 点坐标为(0,2),
点坐标为(0,2),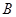 点坐标为(-2,0);
点坐标为(-2,0);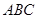 为等腰直角三角形,请画出所有符合条件的点
为等腰直角三角形,请画出所有符合条件的点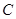 ,并直接写出相应的
,并直接写出相应的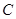 点坐标.
点坐标.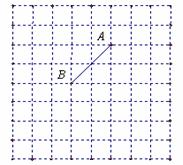
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象上,前面的四种描述正确的是【 】
的图象上,前面的四种描述正确的是【 】| A.①② | B.②③ | C.①④ | D.③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com