
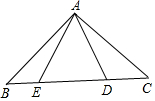
 如图,在△ABC中,∠BAC=90°,AB=AC,点D、E在BC上,且∠DAE=45°,若DE=$\sqrt{15}$,CD=$\sqrt{11}$,则BE=2.
如图,在△ABC中,∠BAC=90°,AB=AC,点D、E在BC上,且∠DAE=45°,若DE=$\sqrt{15}$,CD=$\sqrt{11}$,则BE=2. 分析 将△ABE绕点A逆时针旋转90°得到△ACM.只要证明DE2=BE2+CD2即可解决问题.
解答 解: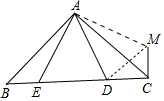 将△ABE绕点A逆时针旋转90°得到△ACM.
将△ABE绕点A逆时针旋转90°得到△ACM.
∵∠BAC=90°,∠EAD=45°,
∴∠BAE+∠ADC=∠DAC+∠CAM=45°,
∴∠DAM=∠DAE=45°,
∵AD=AD,AE=AM,
∴△ADE≌△ADM,
∴DE=DM,
∵∠B=∠ACD=∠ACM=45°,
∴∠DCM=90°,
∴DM2=CD2+CM2,
∵BE=CM,DD=DM,
∴DE2=BE2+CD2,
∵DE=$\sqrt{15}$,CD=$\sqrt{11}$,
∴BE=2.
故答案为2.
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质、勾股定理的等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.


科目:初中数学 来源: 题型:填空题
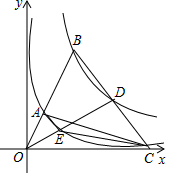 如图,点A为双曲线y=$\frac{2}{x}$(x>0)上一动点,直线OA与双曲线y=$\frac{18}{x}$(x>0)交于点B,点C(9,0),连CB交双曲线y=$\frac{18}{x}$(x>0)于点D,连OD交双曲线y=$\frac{2}{x}$(x>0)于点E,若S△AOC=6S△ACE,则点A坐标为($\frac{9}{7}$,$\frac{14}{9}$).
如图,点A为双曲线y=$\frac{2}{x}$(x>0)上一动点,直线OA与双曲线y=$\frac{18}{x}$(x>0)交于点B,点C(9,0),连CB交双曲线y=$\frac{18}{x}$(x>0)于点D,连OD交双曲线y=$\frac{2}{x}$(x>0)于点E,若S△AOC=6S△ACE,则点A坐标为($\frac{9}{7}$,$\frac{14}{9}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com