
 小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:
小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s (米)与小明出发时间t (分)之间的函数关系如图所示.下列说法:| A. | ①②④ | B. | ①②③ | C. | ①③④ | D. | ①②③④ |
分析 根据小明步行720米,需要9分钟,进而得出小明的运动速度,利用图形得出小华的运动时间以及运动距离进而分别判断得出答案.
解答 解:由图象得出小明步行720米,需要9分钟,
所以小明的运动速度为:720÷9=80(m/分),
当第15分钟时,小华运动15-9=6(分钟),
运动距离为:15×80=1200(m),
∴小华的运动速度为:1200÷6=200(m/分),
∴200÷80=2.5,(故②正确);
当第19分钟以后两人之间距离越来越近,说明小华已经到达终点,则小华先到达青少年宫,(故①正确);
此时小华运动19-9=10(分钟),
运动总距离为:10×200=2000(m),
∴小明运动时间为:2000÷80=25(分钟),
故a的值为25,(故③错误);
∵小明19分钟运动距离为:19×80=1520(m),
∴b=2000-1520=480,(故④正确).
故正确的有:①②④.
故选A.
点评 此题主要考查了一次函数的应用,路程=速度×时间的关系等知识,解题的关键是读懂图象信息,利用数形结合的思想解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,E、F分别是AB、DC上的点,且AE=CF,求证:
如图,在平行四边形ABCD中,E、F分别是AB、DC上的点,且AE=CF,求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
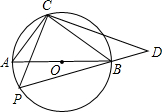 如图,⊙O的直径为6,在⊙O上位于直径AB的异侧有定点C和动点P.已知BC:CA=4:3,P在半圆上运动,CP⊥CD交PB的延长线于D点.当点P运动到什么位置时,△PCD的面积最大为( )
如图,⊙O的直径为6,在⊙O上位于直径AB的异侧有定点C和动点P.已知BC:CA=4:3,P在半圆上运动,CP⊥CD交PB的延长线于D点.当点P运动到什么位置时,△PCD的面积最大为( )| A. | 36 | B. | 24 | C. | 18 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在数轴上点A表示的有理数为-4,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度在数轴上沿由A到B方向运动,当点P到达点B后立即返回,仍然以每秒2个单位长度的速度运动至点A停止运动.设运动时间为t(单位:秒).
如图,在数轴上点A表示的有理数为-4,点B表示的有理数为6,点P从点A出发以每秒2个单位长度的速度在数轴上沿由A到B方向运动,当点P到达点B后立即返回,仍然以每秒2个单位长度的速度运动至点A停止运动.设运动时间为t(单位:秒).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{12}$ | B. | $\frac{1}{32}$ | C. | $\frac{1}{64}$ | D. | $\frac{1}{128}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com