
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
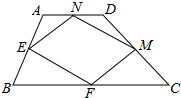
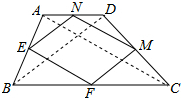 解:连接AC与BD,
解:连接AC与BD,| 1 |
| 2 |
| S△AEN |
| S△ABD |
| EN |
| BD |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
| 朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 6 | 7 | 5 | 7 | 15 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
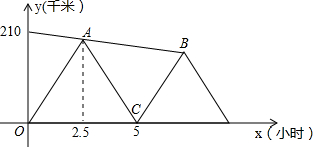 步行速度均近似为匀速,队员上、下车的时间忽略不计).
步行速度均近似为匀速,队员上、下车的时间忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:
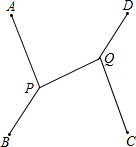 A、B、C、D四个城市恰好为一个正方形的四个顶点,要建立一个公路系统,使每两个城市之间都有公路相通,并使整个公路系统的总长为最小,则这个公路系统应当如何修建?
A、B、C、D四个城市恰好为一个正方形的四个顶点,要建立一个公路系统,使每两个城市之间都有公路相通,并使整个公路系统的总长为最小,则这个公路系统应当如何修建?查看答案和解析>>
科目:初中数学 来源: 题型:
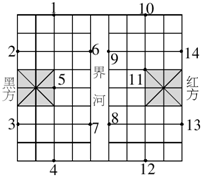 如图,这是一个中国象棋盘,图中小方格都是相同的正方形(“界河”的宽等于小正方形的边长),假设黑方只有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12,13,14中的两个位置,问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?
如图,这是一个中国象棋盘,图中小方格都是相同的正方形(“界河”的宽等于小正方形的边长),假设黑方只有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12,13,14中的两个位置,问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com