
【题目】如图,在平面直角坐标系中,A为y轴正半轴上一点,过点A作x轴的平行线,交函数![]() 的图象于B点,交函数
的图象于B点,交函数![]() 的图象于C,过C作y轴和平行线交BO的延长线于D.
的图象于C,过C作y轴和平行线交BO的延长线于D.
(1)如果点A的坐标为(0,2),求线段AB与线段CA的长度之比;
(2)如果点A的坐标为(0,a),求线段AB与线段CA的长度之比;
(3)在(1)条件下,四边形AODC的面积为多少?

【答案】(1)线段AB与线段CA的长度之比为![]() ;(2)线段AB与线段CA的长度之比为
;(2)线段AB与线段CA的长度之比为![]() ;(3)15.
;(3)15.
【解析】试题分析:
(1)由题意把y=2代入两个反比例函数的解析式即可求得点B、C的横坐标,从而得到AB、AC的长,即可得到线段AB与AC的比值;
(2)由题意把y=a代入两个反比例函数的解析式即可求得用“a”表示的点B、C的横坐标,从而可得到AB、AC的长,即可得到线段AB与AC的比值;
(3)由(1)可知,AB:AC=1:3,由此可得AB:BC=1:4,利用OA=2和平行线分线段成比例定理即可求得CD的长,从而可由梯形的面积公式求出四边形AODC的面积.
试题解析:
(1)∵A(0,2),BC∥x轴,
∴B(﹣1,2),C(3,2),
∴AB=1,CA=3,
∴线段AB与线段CA的长度之比为![]() ;
;
(2)∵B是函数y=﹣![]() (x<0)的一点,C是函数y=
(x<0)的一点,C是函数y=![]() (x>0)的一点,
(x>0)的一点,
∴B(﹣![]() ,a),C(
,a),C(![]() ,a),
,a),
∴AB=![]() ,CA=
,CA=![]() ,
,
∴线段AB与线段CA的长度之比为![]() ;
;
(3)∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
又∵OA=a,CD∥y轴,
∴![]() ,
,
∴CD=4a,
∴四边形AODC的面积为=![]() (a+4a)×
(a+4a)×![]() =15.
=15.


科目:初中数学 来源: 题型:
【题目】在一节数学实践活动课上,老师拿出三个边长都为5cm 的正方形硬纸板,他向同学们提出了这样一个问题:若将三个正方形纸板不重叠地放在桌面上,用一个圆形硬纸板将其盖住,这样的圆形硬纸板的最小直径应有多大?问题提出后,同学们经过讨论,大家觉得本题实际上就是求将三个正方形硬纸板无重叠地适当放置,圆形硬纸板能盖住时的最小直径.老师将同学们讨论过程中探索出的三种不同摆放类型的图形画在黑板上,如图所示:
(1)通过计算(结果保留根号与π).
(Ⅰ)图①能盖住三个正方形所需的圆形硬纸板最小直径应为
(Ⅱ)图②能盖住三个正方形所需的圆形硬纸板最小直径为
(Ⅲ)图③能盖住三个正方形所需的圆形硬纸板最小直径为
(2)其实上面三种放置方法所需的圆形硬纸板的直径都不是最小的,请你画出用圆形硬纸板盖住三个正方形时直径最小的放置方法,(只要画出示意图,不要求说明理由),并求出此时圆形硬纸板的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,P是边AB上的一点,连接CP.
(1)要使△ACP∽△ABC,还需要补充的一个条件是_____.
(2)若△ACP∽△ABC,且AC=![]() ,AB=3,求AP的长.
,AB=3,求AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.
(1)请写出图中各对相似三角形(相似比为1除外);
(2)求BP:PQ:QR.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解学生每天完成家庭作业所用时间的情况,从每班抽取相同数量的学生进行调查,并将所得数据进行整理,制成条形统计图和扇形统计图,如图所示:


(1)补全条形统计图;
(2)求扇形统计图中扇形D的圆心角的度数;
(3)若该中学有2000名学生,请估计其中有多少名学生能在1.5 h内完成家庭作业.
查看答案和解析>>
科目:初中数学 来源: 题型:
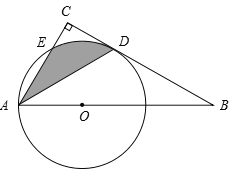
【题目】如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC相切于点D,与AC交于点E,连接AD.
(1)求证:AD平分∠BAC;
(2)若∠BAC = 60°,OA = 2,求阴影部分的面积(结果保留π![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小鹏学完解直角三角形知识后,给同桌小艳出了一道题:“如图所示,把一张长方形卡片ABCD放在每格宽度都为6mm的横格纸中,恰好四个顶点都在横格线上,已知a=36°,求长方形卡片的周长.”请你帮小艳解答这道题.(精确到1mm)(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
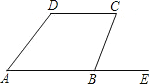
【题目】如图,BE是AB的延长线,指出下面各组中的两个角是由哪两条直线被哪一条直线所截形成的?它们是什么角?
(1)∠A和∠D;
(2)∠A和∠CBA;
(3)∠C和∠CBE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com