
【题目】如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,若PA=6,PB=8,PC=10,则∠APB=_____°.

【答案】150°
【解析】
连结PQ,如图,根据等边三角形的性质得∠BAC=60°,AB=AC,再根据旋转的性质得AP=PQ=6,∠PAQ=60°,则可判断△APQ为等边三角形,所以PQ=AP=6,接着证明△APC≌△ABQ得到PC=QB=10,然后利用勾股定理的逆定理证明△PBQ为直角三角形,于是得到结论.
连结PQ,如图,
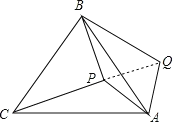
∵△ABC为等边三角形,
∴∠BAC=60![]() ,AB=AC,
,AB=AC,
∵线段AP绕点A顺时针旋转60![]() 得到线段AQ,
得到线段AQ,
∴AP=PQ=6,∠PAQ=60![]() ,
,
∴△APQ为等边三角形,
∴PQ=AP=6,
∵∠CAP+∠BAP=60![]() ,∠BAP+∠BAQ=60
,∠BAP+∠BAQ=60![]() ,
,
∴∠CAP=∠BAQ,
在△APC和△AQB中,
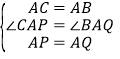 ,
,
∴△APC≌△AQB,
∴PC=QB=10,
在△BPQ中,
∵PB2=82=64,PQ2=62,BQ2=102,
而64+36=100,
∴PB2+PQ2=BQ2,
∴△PBQ为直角三角形,∠BPQ=90![]() ,
,
∴∠APB=90![]() +60
+60![]() =150
=150![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB、BC、DC为边向外作正方形,其面积分别为S1、S2、S3 , 若S1=3,S3=9,则S2的值为( )
A.12
B.18
C.24
D.48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的图象如图所示,下列结论:①abc<0;②2a+b<0;③b2﹣4ac=0;④8a+c<0;⑤a:b:c=﹣1:2:3,其中正确的结论有 . 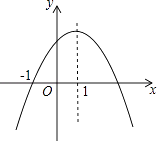
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】英国《![]() ?》杂志最近对30部手机进行了检测,结果发现有近四分之一的手机携带的细菌数量达到可接受数量的10倍,其中一部最脏的手机一度让它的主人出现严重消化不良.在手机上发现的有害细菌中,最为常见的有害细菌当属金黄色葡萄球菌.这种细菌可导致一系列感染,金黄色葡萄球菌为球形,直径
?》杂志最近对30部手机进行了检测,结果发现有近四分之一的手机携带的细菌数量达到可接受数量的10倍,其中一部最脏的手机一度让它的主人出现严重消化不良.在手机上发现的有害细菌中,最为常见的有害细菌当属金黄色葡萄球菌.这种细菌可导致一系列感染,金黄色葡萄球菌为球形,直径![]() 左右,0.0000008米这个数用科学记数法表示为( )
左右,0.0000008米这个数用科学记数法表示为( )
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平分线交⊙O于点D,过点D的切线分别交AB,AC的延长线于E,F,连接BD.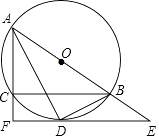
(1)求证:AF⊥EF;
(2)若AC=6,CF=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读下面的数学小探究系列,完成所提出的问题:
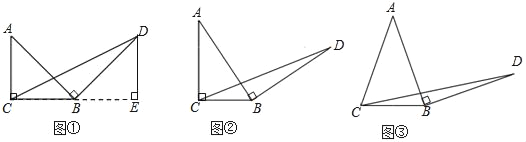
(1)探究1,如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=3,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,过点D做BC边上的高DE,则DE与BC的数量关系是 ,△BCD的面积为 ;
(2)探究2,如图②,在一般的Rt△ABC中,∠ACB=90°,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含a的式子表示△BCD的面积,并说明理由;
(3)探究3:如图③,在等腰三角形ABC中,AB=AC,BC=a,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,试探究用含a的式子表示△BCD的面积,要有探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=ax2+bx﹣4(a≠0)与x轴交于点A(﹣1,0)和点B(4,0).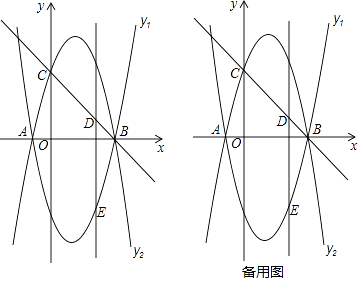
(1)求抛物线y1的函数解析式;
(2)如图①,将抛物线y1沿x轴翻折得到抛物线y2 , 抛物线y2与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线y1于点E,求线段DE的长度的最大值;
(3)在(2)的条件下,当线段DE处于长度最大值位置时,作线段BC的垂直平分线交DE于点F,垂足为H,点P是抛物线y2上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识链接:将两个含30°角的全等三角尺放在一起,让两个30°角合在一起成60°,经过拼凑、观察、思考,探究出“直角三角形中30°角所对的直角边等于斜边的一半”结论.
如图:等边三角形ABC的边长为4cm,点D从点C出发沿CA向A运动,点E从B出发沿AB的延长线BF向右运动,已知点D、E都以每秒0.5cm的速度同时开始运动,运动过程中DE与BC相交于点P,设运动时间为x秒.
(1)请直接写出AD长.(用x的代数式表示)
(2)当△ADE为直角三角形时,运动时间为几秒?
(2)求证:在运动过程中,点P始终为线段DE的中点.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com