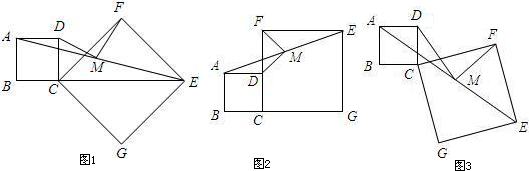
∵正方形ABCD,
∴AD∥BE,AD=DC,∴∠1=∠2
又∵AM=EM,∠3=∠4
∴△ADM≌△ENM
∴AD=EN,MD=MN
又∵AD=DC,∴DC=NE
又∵正方形CGEF,∴∠FCE=∠NEF=45°,FC=FE,∠CFE=90°
又∵正方形ABCD,∴∠BCD=90°.∴∠DCF=∠NEF=45°
∴△FDC≌△FNE∴FD=FN,∠5=∠6
又∵∠CFE=90°,∴∠DFN=90°
又∵DM=MN=

DN,∴M为DN的中点,
∴FM=

DN,∴MD=MF,DM⊥MF
思路一:∵四边形ABCD、CGEF是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠CDA=∠BAD=90°
CF=EF=EG=CG,∠G=∠GEF=∠EFC=∠FCG=90°,∠FCE=∠FEC=45°
∴∠DCF=∠FEC
思路二: 延长DM交CE于N,
∵四边形ABCD、CGEF是正方形∴AD∥CE,∴∠DAM=∠NEM
又∵∠DMA=∠NME,AM=EM,∴△ADM≌△ENM
思路三:∵正方形CGEF,∴∠FCE=∠FEC=45°
又∵正方形ABCD,
∴∠DCB=90°.∴∠DCF=180°﹣∠DCB﹣∠FCE=45°,∠DCF=∠FEC=45°
(2)选取条件① 证明:如图
∵正方形ABCD,∴AD∥BE,AD=DC,∴∠1=∠2
又∵AD=NE,∠3=∠4, ∴△ADM≌△ENM ∴MD=MN
又∵AD=DC,∴DC=NE
又∵正方形CGEF,∴FC=FE,∠FCE=∠FEN=45°.
∴∠FCD=∠FEN=45°
∴△FDC≌△FNE
∴FD=FN,∠5=∠6,∴∠DFN=∠CFE=90°
∴MD=MF,MD⊥MF
选取条件② 证明:如图, 延长DM交FE于N
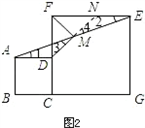
∵正方形ABCD、CGEF
∴CF=EF,AD=DC,∠CFE=90°,AD∥FE.
∴∠1=∠2
又∵MA=ME,∠3=∠4,
∴△AMD≌△EMN
∴MD=MN,AD=EN.∴AD=DC,∴DC=NE
又∵FC=FE,∴FD=FN
又∵∠DFN=90°,
∴FM⊥MD,MF=MD.
选取条件③ 证明:如图, 延长DM交FE于N.
∵正方形ABCD、CGEF
∴CF=EF,AD=DC,∠CFE=90°,AD∥FE ∴∠1=∠2
又∵MA=ME,∠3=∠4,
∴△AMD≌△EMN
∴AD=EN,MD=MN.∴CF=2AD,EF=2EN ∴FD=FN.
又∵∠DFN=90°,
∴MD=MF,MD⊥MF
附加题: 证明:如图
过点E作AD的平行线分别交DM、DC的延长线于N、H,连接DF、FN
∴∠ADC=∠H,∠3=∠4.
∵AM=ME,∠1=∠2,
∴△ADM≌△ENM
∴DM=NM,AD=EN.
∵正方形ABCD、CGEF
∴AD=DC,FC=FE,∠ADC=∠FCG=∠CFE=90°,CG∥FE
∴∠H=90°,∠5=∠NEF,DC=NE
∴∠DCF+∠7=∠5+∠7=90°
∴∠DCF=∠5=∠NEF
∵FC=FE,
∴△DCF≌△NEF
∴FD=FN,∠DFC=∠NFE.
∵∠CFE=90°
∴∠DFN=90°.
∴DM=FM,DM⊥FM.
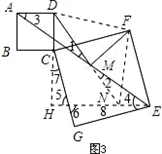

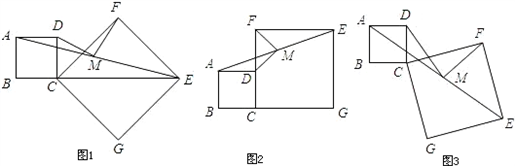

 DN,∴M为DN的中点,
DN,∴M为DN的中点, DN,∴MD=MF,DM⊥MF
DN,∴MD=MF,DM⊥MF



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案