
【题目】甲乙两地相距8000米.张亮骑自行车从甲地出发匀速前往乙地,出发10分钟后,李伟步行从甲地出发同路匀速前往乙地.张亮到达乙地后休息片刻,以原来的速度从原路返回.如图所示是两人离甲地的距离y(米)与李伟步行时间x(分)之间的函数图象.
(1)求两人相遇时李伟离乙地的距离;
(2)请你判断:当张亮返回到甲地时,李伟是否到达乙地?

科目:初中数学 来源: 题型:
【题目】(8分)如图,△A1B1C1是△ABC向右平移四个单位长度后得到的,且三个顶点的坐标分别为A1(1,1),B1(4,2),C1(3,4).
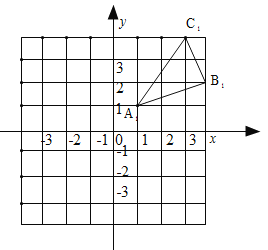
(1)请画出△ABC,并写出点A、B、C的坐标;
(2)求出△AOA1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣4,0),B(2,0),与y轴交于点C(0,4),线段BC的中垂线与对称轴l交于点D,与x轴交于点F,与BC交于点E,对称轴l与x轴交于点H.
(1)求抛物线的函数表达式;
(2)求点D的坐标;
(3)点P为x轴上一点,⊙P与直线BC相切于点Q,与直线DE相切于点R.求点P的坐标;
(4)点M为x轴上方抛物线上的点,在对称轴l上是否存在一点N,使得以点D,P,M.N为顶点的四边形是平行四边形?若存在,则直接写出N点坐标;若不存在,请说明理由.
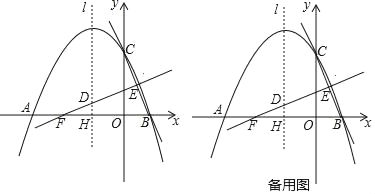
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E在BC边上,且CE︰BC=2︰3,AC与DE相交于点F,若S△EFC=8,则S△CFD=________.
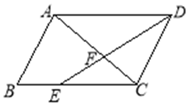
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.
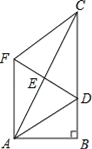
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+bx+c(bc≠0).
(1)若该抛物线的顶点坐标为(c,b),求其解析式;
(2)点A(m,n),B(m+1,![]() n),C(m+6,n)在抛物线y=x2+bx+c上,求△ABC的面积;
n),C(m+6,n)在抛物线y=x2+bx+c上,求△ABC的面积;
(3)在(2)的条件下,抛物线y=x2+bx+c的图象与x轴交于D(x1,0),E(x2,0)(x1<x2)两点,且0<x1+![]() x2<3,求b的取值范围.
x2<3,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
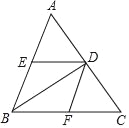
【题目】如图,在△ABC中,DF∥AB,DE∥BC,连接BD.
(1)求证:△DEB≌△BFD;
(2)若点D是AC边的中点,当△ABC满足条件_____时,四边形DEBF为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,G为CD边中点,连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点.已知FG=2,则线段AE的长度为( )
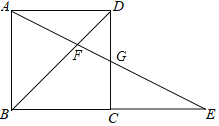
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近来爱好跑步的人越来越多,人们对跑步机的需求也越来越大.图①、②分别是某种型号跑步机的实物图与示意图,已知踏板CD长为1.6m,CD与地面DE的夹角∠CDE为12°,支架AC长为0.8m,∠ACD为80°,则跑步机手柄的一端A的高度h四舍五入到0.1m约为( )(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)

A. 0.9 B. 1.0 C. 1.1 D. 1.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com