
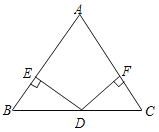
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.
(1)求证:△BED≌△CFD;
(2)若∠A=90°,求证:四边形DFAE是正方形.
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据AB=AC可得∠B=∠C,根据DE⊥AB,DF⊥AC可得∠BED=∠CFD=90°,根据D为中点可得BD=CD,根据AAS可以判定三角形全等;(2)、根据三个角为直角的四边形是矩形,首先得出矩形,然后根据(1)的结论说明有一组邻边相等.
试题解析:(1)、∵AB=AC ∴∠B=∠C ∵DE⊥AB,DF⊥AC ∴∠BED=∠CFD=90°
∵D为BC的中点 ∴BD=CD ∴△BED≌△CFD
(2)、∵DE⊥AB,DF⊥AC ∴∠AED=∠AFD=90° 又∵∠A=90°
∴四边形DFAE为矩形 ∵△BED≌△CFD ∴DE=DF ∴四边形DFAE为正方形.


科目:初中数学 来源: 题型:
【题目】如图,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点E,
点C与点F分别是对应点,观察点与点的坐标之间的关系,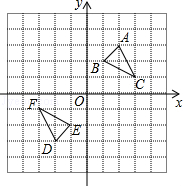
解答下列问题:
(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a,b的值.
(3)求图中△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
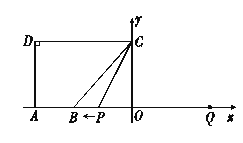
【题目】如图,![]() 点
点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为![]() 秒.
秒.
(1)点![]() 的坐标是 ;
的坐标是 ;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)以点![]() 为圆心,
为圆心,![]() 为半径的
为半径的![]() 随点
随点![]() 的运动而变化,当
的运动而变化,当![]() 与四边形
与四边形![]() 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每件的标价是330元,按标价的八折销售时,仍可获利10%,则这种商品每件的进价为( )
A. 240元 B. 250元 C. 280元 D. 300元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
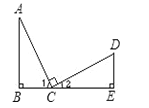
A. ∠1=∠2 B. ∠A =∠2 C. △ABC≌△CED D. ∠A与∠D互为余角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com