
分析 (1)先利用多项式乘法法则把多项式展开,那么原式=x5-3x4+4x3+mx3-3mx2+4mx+nx2-3nx+4n=x5-3x4+(4+m)x3+(-3m+n)x2+(4m-3n)x+4n.由于展开后不含x2项,并且x3的系数为2,由此可以得到4+m=2,-3m+n=0,解方程组即可以求出m、n.
②把m、n的值代入计算即可求解.
解答 解:(1)原式=x5-3x4+4x3+mx3-3mx2+4mx+nx2-3nx+4n
=x5-3x4+(4+m)x3+(-3m+n)x2+(4m-3n)x+4n.
∵不含x2项,并且x3的系数为2,
∴4+m=2,-3m+n=0,
解得m=-2,n=-6;
(2)当m=-2,n=-6时,
(m+n)(m2-mn+n2)
=(-2-6)×(4-12+36)
=-8×28
=-224.
点评 考查了多项式乘以多项式的法则.注意不要漏项,漏字母,有同类项的合并同类项.同时考查了多项式的项的定义.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{3}$+3 | C. | 4$\sqrt{3}$-3 | D. | 4$\sqrt{3}$+3或4$\sqrt{3}$-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
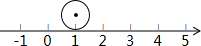 如图,把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与表示1的点重合,圆沿着数轴滚动一周,此时点A表示的数是1-π或1+π..
如图,把半径等于$\frac{1}{2}$的圆放到数轴上,圆上一点A与表示1的点重合,圆沿着数轴滚动一周,此时点A表示的数是1-π或1+π..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com