
如图,点A、B、C分别是⊙O上的点,∠ B=60°, CD是⊙ O的直径,P是CD延长线上的点,且AP=AC.
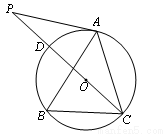
(1)求证:AP是⊙O的切线;
(2)若AC= 3,求PD的长
(1)证明见解析;(2)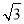
【解析】
试题分析:(1)连接OA,求出∠AOC,求出∠ACP,得出∠P,求出∠AOD,推出∠PAO=90°,根据切线判定推出即可;
(2)根据∠ACD=30°,AC=3求出DC,求出半径,在Rt△PAO中根据勾股定理求出即可.
试题解析:(1)证明:连接OA,
∵∠B=60°,
∴∠AOC=2∠B=120°,
∵OA=OC,
∴∠ACP=∠CAO=30°,
∴∠AOP=60°,
又∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=90°,
即OA⊥AP,
∵点A在⊙O上,
∴AP是⊙O的切线.
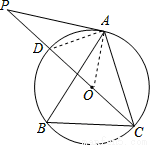
(2)【解析】
连接AD,
∵CD是⊙O的直径,
∴∠CAD=90°,
∴AD=AC?tan30°=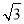 ,CD=2AD=2
,CD=2AD=2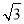 ,
,
∴DO=AO=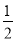 CD=
CD=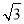 ,
,
在Rt△PAO中,由勾股定理得:PA2+AO2=PO2,
∴32+(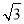 )2=(PD+
)2=(PD+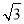 )2,
)2,
∵PD的值为正数,
∴PD=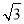 .
.
考点:切线的判定.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源:2014-2015学年山东省九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,将半径为8的⊙O沿AB折叠,弧AB恰好经过与AB垂直的半径OC的中点D,则折痕AB长为( )

A. B.
B.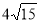 C.8 D.10
C.8 D.10
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期第二次质量抽测数学试卷(解析版) 题型:解答题
已知:如图, AB是⊙O的直径,点C、D为圆上两点,且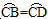 ,CF⊥AB于点F,CE⊥AD的延长线于点E.
,CF⊥AB于点F,CE⊥AD的延长线于点E.

(1)试说明:DE=BF;
(2)若∠DAB=60°,AB=8,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期第二次质量抽测数学试卷(解析版) 题型:选择题
已知实数a、b满足(a2+b2)2-2(a2+b2)=8,则a2+b2的值为 ( )
A.-2 B.4 C.4或-2 D.-4或2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级11月阶段性检测数学试卷(解析版) 题型:解答题
如果一个点能与另外两个点能构成直角三角形,则称这个点为另外两个点的勾股点.例如:矩形ABCD中,点C与A,B两点可构成直角三角形ABC,则称点C为A,B两点的勾股点.同样,点D也是A,B两点的勾股点.
(1)如图1,矩形ABCD中,AB=2,BC=1,请在边CD上作出A,B两点的勾股点(点C和点D除外)(要求:尺规作图,保留作图痕迹,不要求写作法).

(2)矩形ABCD中,AB=3,BC=1,直接写出边CD上A,B两点的勾股点的个数.
(3)如图2,矩形ABCD中,AB=12cm,BC=4cm,DM=8cm,AN=5cm.动点P从D点出发沿着DC方向以1 cm/s的速度向右移动,过点P的直线l平行于BC,当点P运动到点M时停止运动.设运动时间为t(s),点H为M,N两点的勾股点,且点H在直线l上.

①当t=4时,求PH的长.
②探究满足条件的点H的个数(直接写出点H的个数及相应t的取值范围,不必证明).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级11月阶段性检测数学试卷(解析版) 题型:填空题
如图,在矩形ABCD中,AB=2,BC=4,⊙D的半径为1.现将一个直角三角板的直角顶点与矩形的对称中心O重合,绕着O点转动三角板,使它的一条直角边与⊙D切于点H,此时两直角边与AD交于E,F两点,则EH的值为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市宝应县九年级上学期期末测试数学试卷(解析版) 题型:解答题
有A、B两个黑布袋,A布袋中有两个除标号外完全相同的小球,小球上分别标有2、3.B布袋中也有两个除标号外完全相同的小球,小球上分别标有1、2.小明先从A布袋中随机取一个小球,用a表示取出的小球上标有的数字,再从B布袋中取出一个小球,用b表示取出的球上标有的数字.
(1)请你用画树形图法或列表法求出a与b的积为奇数的概率.
(2)关于x的一元二次方程x2-ax+b=0有实数根的概率为 (直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com