
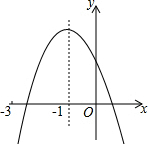
 二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )
二次函数y=ax2+bx+c(a≠0)的图象如图,对称轴x=-1,下列结论:①2a-b=0;②a+b+c<0;③a-b>am2-bm;④a-$\frac{1}{2}$b+$\frac{1}{4}$c>0;⑤ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=-2.其中正确的有( )| A. | ①③④ | B. | ①②④⑤ | C. | ②③⑤ | D. | ①③④⑤ |
分析 ①根据x=-$\frac{b}{2a}=-1$,可得b=2a,所以2a-b=0,据此判断即可.
②根据二次函数y=ax2+bc+c的图象的对称轴是x=-1,与x轴的一个交点A在点(-3,-1)之间,可得与x轴的另一个交点A在点(-1,1)之间,所以x=1时,y<0,据此判断即可.
③根据x=-1时,y取到最大值,最大值是a-b+c,所以对于任意的m≠1,a-b+c>am2-bm+c,所以当m≠1时,a-b>am2-bm,据此判断即可.
④根据二次函数y=ax2+bc+c的图象,可得x=-2时,y>0,所以4a-2b+c>0,所以a-$\frac{1}{2}$b+$\frac{1}{4}$c>0,据此判断即可.
⑤根据对称轴x=-1,可得x1≠x2,x1+x2=-2时,ax12+bx1+c=ax22+bx2+c,所以ax12+bx1=ax22+bx2,据此判断即可.
解答 解:∵x=-$\frac{b}{2a}=-1$,
∴b=2a,
∴2a-b=0,
∴结论①正确.
∵二次函数y=ax2+bc+c的图象的对称轴是x=-1,与x轴的一个交点A在点(-3,-1)之间,
∴与x轴的另一个交点A在点(-1,1)之间,
∴x=1时,y<0,
∴a+b+c<0,
∴结论②正确.
∵x=-1时,y取到最大值,最大值是a-b+c,
∴对于任意的m≠1,a-b+c>am2-bm+c,
∴当m≠1时,a-b>am2-bm,
∴结论③不正确.
∵x=-2时,y>0,
∴4a-2b+c>0,
∴a-$\frac{1}{2}$b+$\frac{1}{4}$c>0,
∴结论④正确.
∵对称轴x=-1,
∴x1≠x2,x1+x2=-2时,有ax12+bx1+c=ax22+bx2+c,
∴ax12+bx1=ax22+bx2,
∴结论⑤正确.
综上,可得
正确的结论有:①②④⑤.
故选:B.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
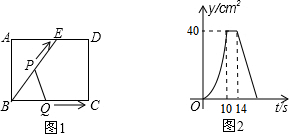
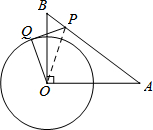 如图,在Rt△OAB中,∠AOB=90°,OA=4,OB=3.⊙O的半径为2,点P是线段AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x,PQ2=y,则y与x的函数图象大致是( )
如图,在Rt△OAB中,∠AOB=90°,OA=4,OB=3.⊙O的半径为2,点P是线段AB上的一动点,过点P作⊙O的一条切线PQ,Q为切点.设AP=x,PQ2=y,则y与x的函数图象大致是( )| A. |  | B. |  | C. | 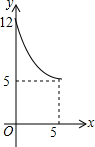 | D. | 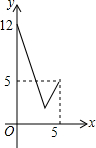 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ②③④ | B. | ①②③ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
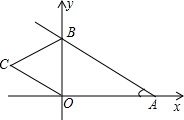 如图,直线y=kx+4与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将△OBCB沿y轴翻折后,点C的对应点C′恰好落在直线AB上,则k的值为-$\frac{\sqrt{3}}{3}$.
如图,直线y=kx+4与x,y轴分别交于A,B两点,以OB为边在y轴左侧作等边三角形OBC,将△OBCB沿y轴翻折后,点C的对应点C′恰好落在直线AB上,则k的值为-$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
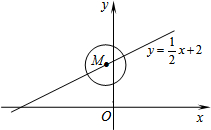 ⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).
⊙M的圆心在一次函数y=$\frac{1}{2}$x+2图象上,半径为1.当⊙M与y轴相切时,点M的坐标为(1,$\frac{5}{2}$)或(-1,$\frac{3}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P 作⊙O的一条切线PQ,Q为切点,则△OPQ面积的最小值为2$\sqrt{2}$.
如图,⊙O是以原点为圆心,$\sqrt{2}$为半径的圆,点P是直线y=-x+6上的一点,过点P 作⊙O的一条切线PQ,Q为切点,则△OPQ面积的最小值为2$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
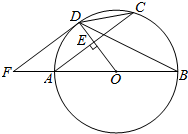 如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,∠CDB=∠BFD.
如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,∠CDB=∠BFD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 海拔/米 | 0 | 100 | 200 | 300 | 400 | … |
| 平均气温/℃ | 24 | 23.4 | 22.8 | 22.2 | 21.6 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com