按要求解下列方程:
(1)(2x-3)2=18 (用直接开平方法) (2)x2+5x-6=0(用配方法)
(3)x2-3=0(用因式分解法) (4)x2+2x-5=0(用公式法)
【答案】
分析:(1)根据完全平方公式,利用直接开平方法解方程;
(2)利用配方法解方程;
(3)利用平方差公式对等式的左边进行因式分解,然后解方程;
(4)利用求根公式解方程.
解答:解:(1)等式的两边同时开平方,得
2x-3=±3
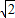
;
∴x=
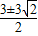
,
∴x
1=
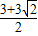
,x
2=
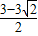
;
(2)由原方程移项,得
x
2+5x=6,
方程的两边同时加上一次项系数的一半的平方,得
x
2+5x+
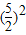
=6+
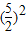
,即

=
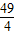
,
∴x=
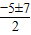
,
∴x
1=-6,x
2=1;
(3)由原方程,得
(x-3)(x+3)=0,
∴x-3=0或x+3=0,
∴x=3或x=-3;
(4)∵方程x
2+2x-5=0的二次项系数a=1,一次项系数b=2,常数项c=-5,
∴x=
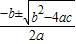
=

=-1±2
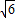
,
∴x
1=-1+2
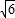
,x
2=-1-2
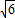
.
点评:本题综合考查了一元二次方程的解法:配方法、因式分解法、公式法以及直接开平方法.在解方程时,要根据方程的特点,灵活选择解方程的方法.

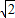 ;
;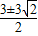 ,
,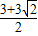 ,x2=
,x2=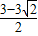 ;
;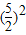 =6+
=6+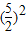 ,即
,即 =
=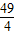 ,
,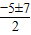 ,
,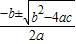 =
= =-1±2
=-1±2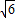 ,
,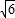 ,x2=-1-2
,x2=-1-2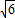 .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案