【题目】一个直角三角形斜边长为
，内切圆半径为
，则这个三角形周长是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
设圆O的半径是r，连接OD，OE，推出正方形DCEO，得出OD=OE=CD=CE，根据切线长定理求出AF=AD，BE=BF，CE=CD，根据AC-r+BC-r=AB求出AC+BC即可．
设圆O的半径是r，连接OD，OE.
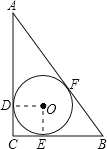
∵圆O与边AC、BC、AB分别切于点D. E.F，
∴OD⊥AC，OE⊥BC，AF=AD，BE=BF，CE=CD，
∵
∴四边形ODCE是正方形，
∴OD=OE=CD=CE，
∴AF=AD=ACr，BF=BE=BCr，
∵AB=AF+BF=(ACr)+(BCr)，
∴ACr+BCr=AB=10cm，
∴AC+BC=12cm，
∴△ABC的周长是：AC+BC+AB=22cm.
故选：B.
举一反三期末百分冲刺卷系列答案科目：初中数学 来源： 题型：
【题目】如图，某消防队在一居民楼前进行演习，消防员利用云梯成功救出点B处的求救者后，又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°，点A距地面2.5米，点B距地面10.5米.为救出点C处的求救者，云梯需要继续上升的高度BC约为多少米？（结果保留整数.参考数据：tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,
≈1.4）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有四张正面分别标有数字2，1，﹣3，﹣4的不透明卡片，它们除数字外其余全部相同，现将它们背面朝上，洗匀后从四张卡片中随机地摸取一张不放回，将该卡片上的数字记为m，再随机地摸取一张，将卡片上的数字记为n．
（1）请画出树状图并写出（m，n）所有可能的结果；
（2）求所选出的m，n能使一次函数y=mx+n的图象经过第二、三、四象限的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
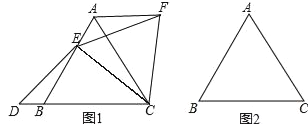
【题目】如图，已知△ABC是等边三角形．
（1）如图（1），点E在线段AB上，点D在射线CB上，且ED=EC．将△BCE绕点C顺时针旋转60°至△ACF，连接EF．猜想线段AB，DB，AF之间的数量关系；
（2）点E在线段BA的延长线上，其它条件与（1）中一致，请在图（2）的基础上将图形补充完整，并猜想线段AB，DB，AF之间的数量关系；
（3）请选择（1）或（2）中的一个猜想进行证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列命题正确的是（ ）
A. 一组对边相等，另一组对边平行的四边形一定是平行四边形
B. 对角线相等的四边形一定是矩形
C. 两条对角线互相垂直的四边形一定是菱形
D. 两条对角线相等且互相垂直平分的四边形一定是正方形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在菱形ABCD中，对角线AC与BD交于点O．过点C作BD的平行线，过点D作AC的平行线，两直线相交于点E．
（1）求证：四边形OCED是矩形；
（2）若CE=1，DE=2，ABCD的面积是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】给出如下定义：对于⊙O 的弦 MN 和⊙O 外一点 P（M，O，N 三点不共线，且点 P，O 在直线 MN 的异侧），当∠MPN+∠MON=180°时，则称点 P 是线段 MN 关于点 O 的关联点．图 1 是点 P 为线段 MN 关于点 O 的关联点的示意图．
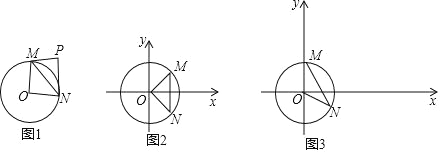
在平面直角坐标系 xOy 中，⊙O 的半径为 1．
（1）如图 2，已知 M（
，），N（ ，﹣），在 A（1，0），B（1，1），C（
，0）三点中，是线段 MN 关于点 O 的关联点的是哪个点；
（2）如图 3，M（0，1），N（
，﹣
），点 D 是线段 MN 关于点 O 的关联点．
①求∠MDN 的大小；
②在第一象限内有一点 E（
m，m），点 E 是线段 MN 关于点 O 的关联点，判断△MNE 的形状，并直接写出点 E 的坐标；
③点 F 在直线 y=﹣
x+2 上，当∠MFN≥∠MDN 时，求点 F 的横坐标 x 的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠C=90°，∠A=30°．
（1）用尺规作图作AB边上的中垂线DE，交AC于点D，交AB于点E．（保留作图痕迹，不要求写作法和证明）；
（2）连接BD，求证：BD平分∠CBA．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
