
分析 (1)根据整式的混合运算顺序和法则可得答案;
(2)根据整式的混合运算顺序和法则可得答案;
(3)根据解一元一次不等式的步骤可得.
解答 解:(1)(-1)×2+(-2)3÷(-4)
=-2+(-8)÷(-4)
=-2+2
=0.
(2)(-3)÷($\frac{3}{2}$)2+$\sqrt{(\frac{1}{3})^{2}}$
=(-3)÷$\frac{9}{4}$+$\frac{1}{3}$
=-$\frac{4}{3}$+$\frac{1}{3}$
=-1.
(3)3x+2>5
3x>3,
x>1.
点评 本题主要考查实数的混合运算能力和解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
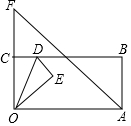 如图,在矩形OABC纸片中,OA=7,OC=5,D为BC边上动点,将△OCD沿OD折叠,当点C的对应点落在直线AF上时,记为点E,若此时连接CE,同时OA=OF,则△OCE面积为$\frac{15}{2}$或10.
如图,在矩形OABC纸片中,OA=7,OC=5,D为BC边上动点,将△OCD沿OD折叠,当点C的对应点落在直线AF上时,记为点E,若此时连接CE,同时OA=OF,则△OCE面积为$\frac{15}{2}$或10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com