
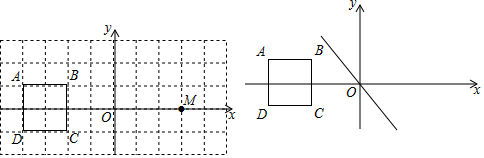
分析 (1)由点P'(-2,2)是点P关于原点O的关联点,可得点P'是线段PO的中点,继而求得答案;
(2)①连接AM,并取中点A′,同理,画出B′、C′、D′;继而求得正方形ABCD关于点M的关联图形;
②首先设N(0,n),易得关联图形的中心Q落在直线y=-x上,然后由正方形ABCD的中心为E(-3,0),求得$\frac{0+n}{2}$=-$\frac{-3+0}{2}$,继而求得答案.
解答 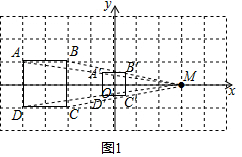 解:(1)∵点P'(-2,2)是点P关于原点O的关联点,
解:(1)∵点P'(-2,2)是点P关于原点O的关联点,
∴点P'是线段PO的中点,
∴点P的坐标是(-4,4);
故答案为:(-4,4);
(2)①如图1,连接AM,并取中点A′;
同理,画出B′、C′、D′;
∴正方形A′B′C′D′为所求作.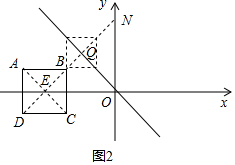 ②如图2,设N(0,n).
②如图2,设N(0,n).
∵正方形ABCD关于点N的关联图形恰好被直线y=-x分成面积相等的两部分,
∴关联图形的中心Q落在直线y=-x上,
∵正方形ABCD的中心为E(-3,0),
∴Q($\frac{-3+0}{2}$,$\frac{0+n}{2}$),
∴代入得:$\frac{0+n}{2}$=-$\frac{-3+0}{2}$,
解得:n=3.
点评 此题属于新定义性题目.考查了一次函数的性质以及关于点的对称图形.注意理解关联图形的定义是关键.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:选择题
| A. | x>-3 | B. | x<-3 | C. | x≠-3 | D. | x≠3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
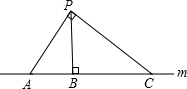 如图所示,P为直线m外一点,点A、B、C在直线m上,且PB⊥m,垂足为B,∠APC=90°,则下列说法错误的是( )
如图所示,P为直线m外一点,点A、B、C在直线m上,且PB⊥m,垂足为B,∠APC=90°,则下列说法错误的是( )| A. | 线段PB的长度叫做点P到直线m的距离 | |
| B. | PA、PB、PC三条线段中,PB最短 | |
| C. | 线段PA的长度叫做点A到直线PC的距离 | |
| D. | 线段AC的长度等于点P到直线m的距离 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
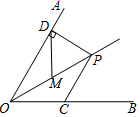 如图,点P在∠AOB的角平分线上,∠AOB=60°,PD⊥OA于D,M在OP上,且DM=MP=4,若C是OB上的动点,则PC的最小值是( )
如图,点P在∠AOB的角平分线上,∠AOB=60°,PD⊥OA于D,M在OP上,且DM=MP=4,若C是OB上的动点,则PC的最小值是( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,下列结论一定成立的是( )
如图,在平行四边形ABCD中,对角线AC与BD相交于点O,下列结论一定成立的是( )| A. | AO=BO | B. | ∠BOC=90° | C. | AD=AC | D. | ∠ADO=∠CBO |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将周长为7cm的△ABC沿BC方向向右平移1cm得到△DEF,则四边形ABFD的周长为( )
如图,将周长为7cm的△ABC沿BC方向向右平移1cm得到△DEF,则四边形ABFD的周长为( )| A. | 7cm | B. | 8cm | C. | 9cm | D. | 10cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com