Question

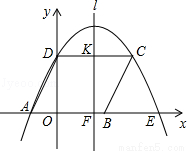
（2013年四川资阳12分）如图，四边形ABCD是平行四边形，过点A、C、D作抛物线y=ax²+bx+c（a≠0），与x轴的另一交点为E，连结CE，点A、B、D的坐标分别为（﹣2，0）、（3，0）、（0，4）．

（1）求抛物线的解析式；

（2）已知抛物线的对称轴l交x轴于点F，交线段CD于点K，点M、N分别是直线l和x轴上的动点，连结MN，当线段MN恰好被BC垂直平分时，求点N的坐标；

（3）在满足（2）的条件下，过点M作一条直线，使之将四边形AECD的面积分为3：4的两部分，求出该直线的解析式．

 

Answer 1

【答案】

解：（1）∵点A、B、D的坐标分别为（﹣2，0）、（3，0）、（0，4），且四边形ABCD是平行四边形，

∴AB=CD=5。∴点C的坐标为（5，4）。

∵抛物线y=ax²+bx+c（a≠0）过点A、C、D，

∴，解得]。

∴抛物线的解析式为。

（2）连接BD交对称轴于G，

      在Rt△OBD中，易求BD=5，

∴CD=BD，则∠DCB=∠DBC。

又∵∠DCB=∠CBE，∴∠DBC=∠CBE。

过G作GN⊥BC于H，交x轴于N，易证GH=HN，

∴点G与点M重合。

∴直线BD的解析式。 

根据抛物线可知对称轴方程为x=，

则点M的坐标为（，），即GF= MF=，BF=。

∴。

又∵MN被BC垂直平分，∴BM=BN=。∴BN=OB+BN=3+。

∴点N的坐标为（，0）。

（3）过点M作直线交x轴于点P₁，

易求四边形AECD的面积为28，四边形ABCD的面积为20，

由“四边形AECD的面积分为3：4”可知直线P₁M必与线段CD相交，

设交点为Q₁，四边形AP₁Q₁D的面积为S₁，四边形P₁ECQ₁的面积为S₂，点P₁的坐标为（a，0），则S₂=12。

若点P在对称轴的左侧，则P₁F=﹣a，P₁E=7﹣a，

由△MKQ₁∽△MFP₁，得。∴Q₁K=5P₁F=5（﹣a）。

∴CQ₁=﹣5（﹣a）=5a﹣10。

∴。∴。

根据P₁（，0），M（，）可求直线P₁M的解析式为。

若点P在对称轴的右侧，同理可得直线P₂M的解析式为。

综上所述，该直线的解析式为或。

【解析】（1）根据平行四边形的性质可求点C的坐标，由待定系数法即可求出抛物线的解析式。

（2）连接BD交对称轴于G，过G作GN⊥BC于H，交x轴于N，根据待定系数法即可求出直线BD的解析式，根据抛物线对称轴公式可求对称轴，由此即可求出点N的坐标。

（3）过点M作直线交x轴于点P₁，分点P在对称轴的左侧，点P在对称轴的右侧，两种情况讨论即可求出直线的解析式。

考点：二次函数综合题，双动点问题，4待定系数法的应用，曲线上点的坐标与方程的关系，平行四边形的性质，二次函数的性质，勾股定理，相似三角形的判定和性质，分类思想的应用。