
【题目】在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.
(1)求∠EFD的度数;
(2)判断FE与FD之间的数量关系,并证明你的结论.
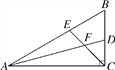
【答案】(1)120°;(2)FE=FD. 见解析
【解析】试题分析:(1)根据三角形内角和定理和角平分线的定义计算求解;
(2)在AC上截取AG=AE,则EF=FG;根据ASA证明△FGC≌△FDC,得DF=FG,故判断EF=FD.
试题解析:(1)∵△ABC中,∠ACB=90°,∠B=60°,
∴∠BAC=30°.
∵AD,CE分别是∠BAC和∠BCA的平分线,
∴∠FAC=![]() ∠BAC=15°,∠FCA=
∠BAC=15°,∠FCA=![]() ∠ACB=45°.
∠ACB=45°.
∴∠AFC=180°-∠FAC-∠FCA=120°,
∴∠EFD=∠AFC=120°.
(2)结论:FE=FD.
证明:如图,在AC上截取AG=AE,连接FG,
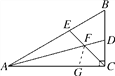
∵AD是∠BAC的平分线,
∴∠EAF=∠GAF.在△FAE和△FAG中,
AE=AG,∠EAF=∠GAF,AF=AF,
∴△AEF≌△AGF(SAS),
∴FE=FG,∠AFE=∠AFG.
∵∠EFD=120°,
∴∠DFC=60°,∠AFG=∠AFE=60°,
∴∠CFG=60°=∠DFC.
∵EC平分∠BCA,
∴∠DCF=∠FCG=45°.
在△FGC和△FDC中,
∵∠GFC=∠DFC,FC=FC,∠FCG=∠FCD,
∴△FGC≌△FDC(ASA),
∴FG=FD,
∴FE=FD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直角三角形ABC的直角边AB=6,BC=8,将直角三角形ABC沿边BC的方向平移到三角形DEF的位置,DE交AC于点G,BE=2,三角形CEG的面积为13.5,下列结论:
①三角形ABC平移的距离是4; ②EG=4.5;
③AD∥CF; ④四边形ADFC的面积为6.
其中正确的结论是( )

A. ①② B. ②③ C. ③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)(x3)2.(﹣x4)3 (2)(![]() x5y4﹣
x5y4﹣![]() x4y3)
x4y3)![]() x3y3
x3y3
(3)2mn.[(2mn)2﹣3n(mn+m2n)] (4)(2a+1)2﹣(2a+1)(2a﹣1)
(5)102+![]() ×(π﹣3.14)0﹣|﹣302|
×(π﹣3.14)0﹣|﹣302|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB∥CD,

求:(1)在图(1)中∠B+∠D=?(2)在图(2)中∠B+∠E1+∠D=?(3)在图(3)中∠B+∠E1+∠E2+…+∠En﹣1+∠En+∠D=?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车和一辆摩托车分别从A,B两地去同一个城市,它们离A地的路程随时间变化的图象如图所示.则下列结论:①摩托车比汽车晚到1h;②A,B两地的路程为20km;③摩托车的速度为45km/h,汽车的速度为60km/h;④汽车出发1小时后与摩托车相遇,此时距B地40千米.其中正确结论的个数是( )
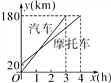
A. 2个 B. 3个 C. 4个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12cm,宽OB为4cm,隧道顶端D到路面的距离为10cm,建立如图所示的直角坐标系 
(1)求该抛物线的解析式.
(2)一辆货运汽车载一长方体集装箱,集装箱最高处与地面距离为6m,宽为4m,隧道内设双向行车道,问这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面高度相等,如果灯离地面的高度不超过8.5m,那么两排灯的水平距离最小是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼外墙有高为AB的广告牌,由距离大楼20米的点C(即CD=20米)观察它的顶部A的仰角是55°,底部B的仰角是42°,求AB的高度.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com