
【题目】如图,抛物线y=ax2+bx+1过A(1,0)、B,(5,0)两点.
(1)求:抛物线的函数表达式;
(2)求:抛物线与y轴的交点C的坐标及其对称轴
(3)若抛物线对称轴上有一点P,使△COA∽△APB,求点P的坐标.
【答案】
(1)
解:∵抛物线y=ax2+bx+1过A(1,0)、B,(5,0)两点,
∴ ![]() ,解得
,解得 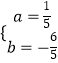 ,
,
∴抛物线的函数表达式为y= ![]() x2﹣
x2﹣ ![]() x+1
x+1
(2)
解:在y= ![]() x2﹣
x2﹣ ![]() x+1中,令x=0可得y=1,
x+1中,令x=0可得y=1,
∴C点坐标为(0,1),
又y= ![]() x2﹣
x2﹣ ![]() x+1=
x+1= ![]() (x﹣3)2﹣
(x﹣3)2﹣ ![]() ,
,
∴抛物线对称轴为直线x=3
(3)
解:∵A(1,0),C(0,1),
∴OA=OC=1,
∴△COA为等腰直角三角形,且∠COA=90°,
∵△COA∽△APB,
∴△APB为等腰直角三角形,∠APB=90°,
∵P在抛物线对称轴上,
∴P到AB的距离= ![]() AB=
AB= ![]() ×(5﹣1)=2,
×(5﹣1)=2,
∴P点坐标为(3,2)或(3,﹣2)
【解析】(1)把A、B两点坐标代入,可求得a、b的值,可求得抛物线的函数表达式;(2)根据(1)中所求抛物线的解析式可求得C点的坐标,及对称轴;(3)由A、C点的坐标可判定△COA为等腰直角三角形,若△COA∽△APB,可知△APB为等腰直角三角形,利用直角三角形的性质可求得P到x轴的距离,可求得P点坐标.
【考点精析】通过灵活运用二次函数的性质和相似三角形的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;对应角相等,对应边成比例的两个三角形叫做相似三角形即可以解答此题.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】某校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分为四类(A.特别好,B.好,C.一般,D.较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题: 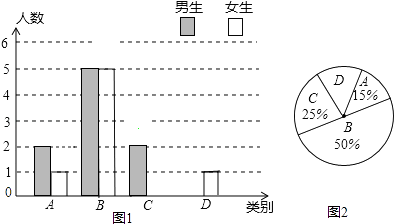
(1)本次调查中,王老师一共调查了名学生;
(2)将两幅统计图中不完整的部分补充完整;
(3)假定全校各班实施新课程改革效果一样,全校共有学生2 400人,请估计该校新课程改革效果达到A类的有多少学生;
(4)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱底面半径为![]() cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A. 12cm B. ![]() cm C. 15cm D.
cm C. 15cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,OA=OB,∠AOB=50°,将△AOB绕O点顺时针旋转30°,得到△COD,OC交AB于点F,CD分别交AB、OB于点E、H.求证:EF=EH. 
查看答案和解析>>
科目:初中数学 来源: 题型:
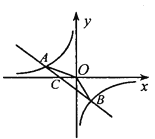
【题目】如图,已知A(-4,n),B(2,-4)是一次函数![]() 的图像和反比例函数
的图像和反比例函数![]() 的图像的两个交点.
的图像的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求不等式![]() 的解集_________(请直接写出答案).
的解集_________(请直接写出答案).
(3)求△AOB的面积;
查看答案和解析>>
科目:初中数学 来源: 题型:
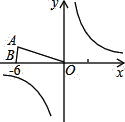
【题目】已知:等腰△OAB在直角坐标系中的位置如图,点A坐标为![]() ,点B坐标为(-6,0).
,点B坐标为(-6,0).
(1)若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数![]() 的图象上,求a的值;
的图象上,求a的值;
(2)若△OAB绕点O按逆时针方向旋转α度(0<α<360).
①当α=30°时,点B恰好落在反比例函数![]() 的图象上,求k的值;
的图象上,求k的值;
②问点A、B能否同时落在①中的反比例函数的图象上?若能,直接写出α的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据如下解方程![]() =
=![]() 的过程,仿照实例在每个步骤前面的括号内填写该步骤的名称,后面的括号内填写这样变形的依据,在最后的横线上写出方程的解.
的过程,仿照实例在每个步骤前面的括号内填写该步骤的名称,后面的括号内填写这样变形的依据,在最后的横线上写出方程的解.
解:原方程可变形为![]() .(分数的基本性质)
.(分数的基本性质)
去分母,得3(3x+5)=2(x–1).(__________)
去括号,得9x+15=2x–2.(__________)
(__________),得9x–2x=–15–2.(__________)
合并同类项,得7x=–17.
(__________),得x=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司员工分别住在A、B、C、D四个住宅区,A区有20人,B区有15人,C区有5人,D区有30人,四个区在同一条直线上,位置如图所示.该公司的接送车打算在此间设立一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设置在( )
![]()
A. D区 B. A区 C. AB两区之间 D. BC两区之间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com