
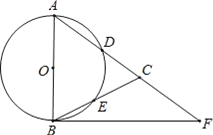
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.
【答案】(1)(2)见解析
【解析】(1)连接AE,利用直径所对的圆周角是直角,从而判定直角三角形,利用直角三角形两锐角相等得到直角,从而证明∠ABF=90°.
(2)利用已知条件证得△AGC∽△ABF,利用比例式求得线段的长即可.
(1)证明:连接AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠1+∠2=90°.
∵AB=AC,
∴∠1=![]() ∠CAB.
∠CAB.
∵∠CBF=![]() ∠CAB,
∠CAB,
∴∠1=∠CBF
∴∠CBF+∠2=90°
即∠ABF=90°
∵AB是⊙O的直径,
∴直线BF是⊙O的切线.
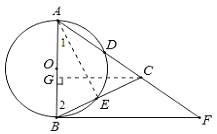
(2)解:过点C作CG⊥AB于G.
∵sin∠CBF=![]() ,∠1=∠CBF,
,∠1=∠CBF,
∴sin∠1=![]() ,
,
∵在Rt△AEB中,∠AEB=90°,AB=5,
∴BE=ABsin∠1=![]() ,
,
∵AB=AC,∠AEB=90°,
∴BC=2BE=2![]() ,
,
在Rt△ABE中,由勾股定理得AE=![]() =2
=2![]() ,
,
∴sin∠2=![]() =
=![]() =
=![]() ,cos∠2=
,cos∠2=![]() =
=![]() =
=![]() ,
,
在Rt△CBG中,可求得GC=4,GB=2,
∴AG=3,
∵GC∥BF,
∴△AGC∽△ABF,
∴![]() =
=![]() .
.
∴BF=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,已知A(﹣1,0)、B(3,0)、C(0,﹣1)三点,D(1,m)是一个动点,当△ACD的周长最小时,△ABD的面积为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①已知直角三角形的面积为4,两直角边的比为1:2,则斜边长为 ![]() ;②直角三角形的最大边长为
;②直角三角形的最大边长为 ![]() ,最短边长为1,则另一边长为
,最短边长为1,则另一边长为 ![]() ;③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC为直角三角形;④等腰三角形面积为12,底边上的高为4,则腰长为5,其中正确结论的序号是( )
;③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC为直角三角形;④等腰三角形面积为12,底边上的高为4,则腰长为5,其中正确结论的序号是( )
A.只有①②③
B.只有①②④
C.只有③④
D.只有②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,最适合采用普查的是( )
A.了解一批灯泡的使用寿命B.了解中央电视台《最强大脑》栏目的收视率
C.了解全国中学生体重情况D.了解某班学生对“七步洗手法”的知晓率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F,G分别是AD,CD,BC上的点,且BE=EF,BE⊥EF,EG⊥BF.若FC=1,AE=2,则BG的长是( )
A.2.6
B.2.5
C.2.4
D.2.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com