
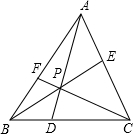
 已知P为△ABC内任意一点,连AP,BP,CP并延长分别交对边于D,E,F.
已知P为△ABC内任意一点,连AP,BP,CP并延长分别交对边于D,E,F.| PD |
| AD |
| PE |
| BE |
| PF |
| CF |
| AP |
| AD |
| BP |
| PE |
| CP |
| PF |
| PD |
| AD |
| PE |
| BE |
| PF |
| CF |
| 1 |
| 3 |
| PD |
| AD |
| 1 |
| 3 |
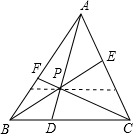 解:(1)由面积概念得:
解:(1)由面积概念得:| S△PBC |
| S△ABC |
| S△PAC |
| S△ABC |
| S△PAB |
| S△ABC |
| S△PDC |
| S△ADC |
| PD |
| AD |
| S△PDB |
| S△ADB |
| PD |
| AD |
| S△PDC+S△PDB |
| S△ADC+S△ADB |
| PD |
| AD |
| S△PBC |
| S△ABC |
| PD |
| AD |
| S△PAC |
| S△ABC |
| PE |
| BE |
| S△PAB |
| S△ABC |
| PF |
| CF |
| PD |
| AD |
| PE |
| BE |
| PF |
| CF |
| PD |
| AD |
| PE |
| BE |
| PF |
| CF |
| PD |
| AD |
| PE |
| BE |
| PF |
| CF |
| 1 |
| 3 |
| PD |
| AD |
| 1 |
| 3 |
| AP |
| PD |
| AP |
| PD |


科目:初中数学 来源:新教材完全解读 七年级数学 (下册) (配人教版新课标) (第1次修订版) 配人教版新课标 题型:047
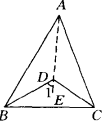
如图所示,已知D为△ABC内任一点.试说明∠BDC>∠ABD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com