练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．不等式3x-6＞0的最小整数解是3．

    分析 首先利用不等式的基本性质解不等式，再从不等式的解集中找出适合条件的最小整数即可．

    解答 解：移项得：3x＞6，
    系数化为1，得：x＞2，
    ∴不等式3x-6＞0的最小整数解是3，
    故答案为：3．

    点评 本题考查了解一元一次不等式、不等式的整数解、不等式的基本性质的应用，解此题的关键是求出不等式的解集．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    19．下列说法中，正确的是（　　）
    A．“打开电视机，正在播放体育节目”是必然事件
    B．检测某校早餐奶的质量，应该采用抽样调查的方式
    C．某同学连续10次投掷质量均匀的硬币，3次正面向上，因此正面向上的概率是30%
    D．在连续5次数学测试中，两名同学的平均分相同，方差较大的同学数学成绩更稳定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

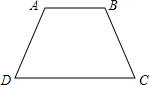    20．我们把：“有一组邻角相等的凸四边形”叫做“等邻角四边形”．
    （1）任意写出你所学过的特殊四边形中是“等邻角四边形”的一种图形的名称；
    （2）在探究“等邻角四边形”性质时：
    ①小明画了一个“等邻角四边形”ABCD（如图1），其中∠A=∠B，AD=BC，此时他发现AB∥DC，请你证明此结论；
    ②由此小明猜想：“对于任意等邻角四边形，当一组对边相等时，另一组对边就平行”，请你直接判断这个命题是真命题还是假命题；
    （3）已知：在“等邻角四边形”ABCD中，∠A=90°，∠C=60°，AB=6，BC=10，请画出相应图形，并直接写出CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．若y=$\sqrt{x-2}$+$\sqrt{2-x}$-3，则代数式x+y的值=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．已知P1（2，y1），P2（3，y2）是正比例函数y=-2x的图象上的两点，则y1＞y2．（填“＞”或“＜”或“=”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图，正方形ABCD中，点P以1cm/s的速度从点A出发按箭头方向运动，到达点D停止，△PAD的面积y（cm2）与运动时间x（s）之间的函数关系如图所示．（规定：点P在点A、D时，y=0）
    发现：
    （1）AB=6cm，当x=17（s）时，y=3cm2；
    （2）当点P在线段BC上运动时，y的值保持不变；
    拓展：求当0＜x＜6及12＜x＜18时，y与x之间的函数关系式．
    探究：当x（s）的值为多少时，y的值等于15cm2？

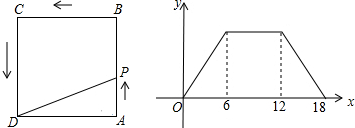
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

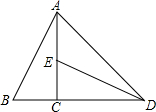    1．如图所示，将Rt△ABC绕其直角顶点C按顺时针方向旋转90°后得到Rt△DEC，连接AD，若∠BAC=25°，则∠ADE=（　　）
    A．20°B．25°C．30°D．35°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

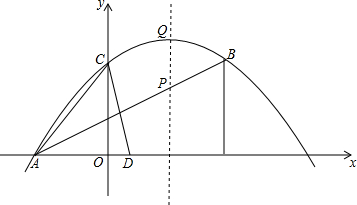    18．如图，抛物线y=ax2+bx+4的图象经过A（-3，0），B（5，4），与y轴交于点C．
    （1）求抛物线的解析式；
    （2）线段AB在第一象限内的部分上有一动点P，过点P作y轴的平行线，交抛物线于点Q，是否存在点P使四边形BPCQ的面积最大？如果存在，请求出点P的坐标及面积的最大值；如果不存在，说明理由；
    （3）x轴正半轴上有一点D（1，0），线段AC上是否存在点M，使△AOM∽△ADC？如果存在，直接写出点M的坐标；如果不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．在正方形ABCD中，对角线AC、BD交于点O，点P在线段BC上（不与点B重合），E在BO上，且∠BPE=$\frac{∠BCA}{2}$，过点B作PE交PE的延长线于F，交AC于点G．

    （1）当点P与点C重合时（如图1），填空△BOG≌△POE，$\frac{BF}{PE}$=$\frac{1}{2}$；
    （2）当点P不与点C重合时（图2），猜想：$\frac{BF}{PE}$的值为$\frac{1}{2}$．并证明你的结论；
    （3）把正方形ABCD改为菱形，其他条件不变（如图3），若∠ACB=α，则直接写出的值为．（用含α的式子表示）

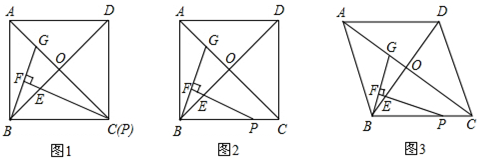
    查看答案和解析>>

    同步练习册答案