
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯп![]() ЕФЖЅЕу
ЕФЖЅЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЎ
ЩЯЃЎ
ЃЈ1ЃЉЧѓжБЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЯжНЋХзЮяЯпбиИУжБЯпЗНЯђНјааЦНвЦЃЌЦНвЦКѓЕФХзЮяЯпЕФЖЅЕуЮЊЕу![]() ЃЌгыжБЯпЕФСэвЛИіНЛЕуЮЊЕу
ЃЌгыжБЯпЕФСэвЛИіНЛЕуЮЊЕу![]() ЃЌгы
ЃЌгы![]() жсЕФгвНЛЕуЮЊЕу
жсЕФгвНЛЕуЮЊЕу![]() ЃЈЕу
ЃЈЕу![]() ВЛгыЕу
ВЛгыЕу![]() жиКЯЃЉЃЌСЌНг
жиКЯЃЉЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЂйШчЭМЃЌдкЦНвЦЙ§ГЬжаЃЌЕБЕу![]() дкЕкЫФЯѓЯоЧв
дкЕкЫФЯѓЯоЧв![]() ЕФУцЛ§ЮЊ60ЪБЃЌЧѓЦНвЦЕФОрРы
ЕФУцЛ§ЮЊ60ЪБЃЌЧѓЦНвЦЕФОрРы![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЂкдкЦНвЦЙ§ГЬжаЃЌЕБ![]() ЪЧвдЯпЖЮ
ЪЧвдЯпЖЮ![]() ЮЊвЛЬѕжБНЧБпЕФжБНЧШ§НЧаЮЪБЃЌЧѓГіЫљгаТњзуЬѕМўЕФЕу
ЮЊвЛЬѕжБНЧБпЕФжБНЧШ§НЧаЮЪБЃЌЧѓГіЫљгаТњзуЬѕМўЕФЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЂй
ЃЛЃЈ2ЃЉЂй![]() ЃЌЂк
ЃЌЂк![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
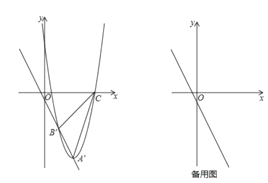
ЃЈ1ЃЉРћгУХфЗНЗЈНЋХзЮяЯпБэДяЪНБфаЮЮЊЖЅЕуЪНЃЌгЩДЫПЩЕУГіЕуAЕФзјБъЃЌИљОнЕуAЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіжБЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЩшЕуAЁфЕФзјБъЮЊЃЈmЃЌЉ2mЉ2ЃЉЃЌдђЦНвЦКѓХзЮяЯпЕФКЏЪ§БэДяЪНЮЊyЃН![]() ЃЈxЉmЃЉ2Љ2mЉ2ЃЌРћгУвЛДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїНсКЯЕуCдкxжсЩЯЧвЕуCВЛгыЕуAЁфжиКЯЃЌПЩЕУГіmЃОЉ1ЃЎ
ЃЈxЉmЃЉ2Љ2mЉ2ЃЌРћгУвЛДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїНсКЯЕуCдкxжсЩЯЧвЕуCВЛгыЕуAЁфжиКЯЃЌПЩЕУГіmЃОЉ1ЃЎ
ЂйСЊСЂжБЯпКЭХзЮяЯпЕФБэДяЪНГЩЗНГЬзщЃЌЭЈЙ§НтЗНГЬзщПЩЧѓГіЕуBЁфЕФзјБъЃЌРћгУЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЧѓГіЕуCЕФзјБъЃЌЙ§ЕуCзїCDЁЮyжсЃЌНЛжБЯпAЁфBЁфгкЕуDЃЌгЩЕуCЕФзјБъПЩЕУГіЕуDЕФзјБъЃЌРћгУSЁїAЁфBЁфCЃНSЁїBЁфCDЉSЁїAЁфCDЃН60ЃЌМДПЩЕУГіЙигкtЕФЗНГЬЃЌРћгУЛЛдЊЗЈНтЗНГЬзщМДПЩЕУГіmЕФжЕЃЌНјЖјПЩЕУГіЕуAЁфЕФзјБъЃЌдйгЩЕуAЕФзјБъРћгУСНЕуМфЕФОрРыЙЋЪНМДПЩЧѓГіНсТлЃЛ
ЂкИљОнЕуAЁфЁЂBЁфЁЂCЕФзјБъЃЌПЩЕУГіAЁфBЁфЁЂAЁфCЁЂBЁфCЕФГЄЖШЃЌЗжЁЯAЁфBЁфCЃН90ЁуМАЁЯBЁфAЁфCЃН90ЁуСНжжЧщПіЃЌРћгУЙДЙЩЖЈРэПЩЕУГіЙигкmЕФЗНГЬЃЌРћгУЛЛдЊЗЈНтЗНГЬМДПЩЧѓГіmЕФжЕЃЌНјЖјПЩЕУГіЕуAЁфЕФзјБъЃЌДЫЬтЕУНтЃЎ
ЃЈ1ЃЉЁпyЃН![]() Љ6x+4ЃН
Љ6x+4ЃН![]() ЃЈxЉ6ЃЉ2Љ14ЃЌ
ЃЈxЉ6ЃЉ2Љ14ЃЌ
ЁрЕуAЕФзјБъЮЊЃЈ6ЃЌЉ14ЃЉЃЎ
ЁпЕуAдкжБЯпyЃНkxЉ2ЩЯЃЌ
ЁрЉ14ЃН6kЉ2ЃЌНтЕУЃКkЃНЉ2ЃЌ
ЁржБЯпЕФКЏЪ§БэДяЪНЮЊyЃНЉ2xЉ2ЃЎ
ЃЈ2ЃЉЩшЕуAЁфЕФзјБъЮЊЃЈmЃЌЉ2mЉ2ЃЉЃЌдђЦНвЦКѓХзЮяЯпЕФКЏЪ§БэДяЪНЮЊyЃН![]() ЃЈxЉmЃЉ2Љ2mЉ2ЃЎ
ЃЈxЉmЃЉ2Љ2mЉ2ЃЎ
ЕБyЃН0ЪБЃЌгаЉ2xЉ2ЃН0ЃЌ
НтЕУЃКxЃНЉ1ЃЌ
ЁпЦНвЦКѓЕФХзЮяЯпгыxжсЕФгвНЛЕуЮЊCЃЈЕуCВЛгыЕуAЁфжиКЯЃЉЃЌ
ЁрmЃОЉ1ЃЎ
ЂйСЊСЂжБЯпгыХзЮяЯпЕФБэДяЪНГЩЗНГЬзщЃЌ 
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЕуBЁфЕФзјБъЮЊЃЈmЉ4ЃЌЉ2m+6ЃЉЃЎ
ЕБyЃН0ЪБЃЌга![]() ЃЈxЉmЃЉ2Љ2mЉ2ЃН0ЃЌ
ЃЈxЉmЃЉ2Љ2mЉ2ЃН0ЃЌ
НтЕУЃКx1ЃНmЉ2![]() ЃЌx2ЃНm+2
ЃЌx2ЃНm+2![]() ЃЌ
ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈm+2![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
Й§ЕуCзїCDЁЮyжсЃЌНЛжБЯпAЁфBЁфгкЕуDЃЌШчЭМЫљЪОЃЎ
ЕБxЃНm+2![]() ЪБЃЌyЃНЉ2xЉ2ЃНЉ2mЉ4
ЪБЃЌyЃНЉ2xЉ2ЃНЉ2mЉ4![]() Љ2ЃЌ
Љ2ЃЌ
ЁрЕуDЕФзјБъЮЊЃЈm+2![]() ЃЌЉ2mЉ4
ЃЌЉ2mЉ4![]() Љ2ЃЉЃЌ
Љ2ЃЉЃЌ
ЁрCDЃН2m+2+4![]() ЃЎ
ЃЎ
ЁрSЁїAЁфBЁфCЃНSЁїBЁфCDЉSЁїAЁфCDЃН![]() CD[m+2
CD[m+2![]() ЉЃЈmЉ4ЃЉ]Љ
ЉЃЈmЉ4ЃЉ]Љ![]() CDЃЈm+2
CDЃЈm+2![]() ЉmЃЉЃН2CDЃН2ЃЈ2m+2+4
ЉmЃЉЃН2CDЃН2ЃЈ2m+2+4![]() ЃЉЃН60ЃЎ
ЃЉЃН60ЃЎ
ЩшtЃН![]() ЃЌдђгаt2+2tЉ15ЃН0ЃЌ
ЃЌдђгаt2+2tЉ15ЃН0ЃЌ
НтЕУЃКt1ЃНЉ5ЃЈЩсШЅЃЉЃЌt2ЃН3ЃЌ
ЁрmЃН8ЃЌ
ЁрЕуAЁфЕФзјБъЮЊЃЈ8ЃЌЉ18ЃЉЃЌ
ЁрAAЁфЃН![]() ЃЎ
ЃЎ
ЂкЁпAЁфЃЈmЃЌЉ2mЉ2ЃЉЃЌBЁфЃЈmЉ4ЃЌЉ2m+6ЃЉЃЌCЃЈm+2![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
ЁрAЁфBЁф2ЃНЃЈmЉ4ЉmЃЉ2+[Љ2m+6ЉЃЈЉ2mЉ2ЃЉ]2ЃН80ЃЌAЁфC2ЃНЃЈm+2![]() ЉmЃЉ2+[0ЉЃЈЉ2mЉ2ЃЉ]2ЃН4m2+12m+8ЃЌBЁфC2ЃН[m+2
ЉmЃЉ2+[0ЉЃЈЉ2mЉ2ЃЉ]2ЃН4m2+12m+8ЃЌBЁфC2ЃН[m+2![]() ЉЃЈmЉ4ЃЉ]2+[0ЉЃЈЉ2m+6ЃЉ]2ЃН4m2Љ20m+56+16
ЉЃЈmЉ4ЃЉ]2+[0ЉЃЈЉ2m+6ЃЉ]2ЃН4m2Љ20m+56+16![]() ЃЎ
ЃЎ
ЕБЁЯAЁфBЁфCЃН90ЁуЪБЃЌгаAЁфC2ЃНAЁфBЁф2+BЁфC2ЃЌМД4m2+12m+8ЃН80+4m2Љ20m+56+16![]() ЃЌ
ЃЌ
ећРэЕУЃК32mЉ128Љ16![]() ЃН0ЃЎ
ЃН0ЃЎ
ЩшaЃН![]() ЃЌдђга2a2ЉaЉ10ЃН0ЃЌ
ЃЌдђга2a2ЉaЉ10ЃН0ЃЌ
НтЕУЃКa1ЃНЉ2ЃЈЩсШЅЃЉЃЌa2ЃН![]() ЃЌ
ЃЌ
ЁрmЃН![]() ЃЌ
ЃЌ
ЁрЕуAЁфЕФзјБъЮЊ![]() ЃЛ
ЃЛ
ЕБЁЯBЁфAЁфCЃН90ЁуЪБЃЌгаBЁфC2ЃНAЁфBЁф2+AЁфC2ЃЌМД4m2Љ20m+56+16![]() ЃН80+4m2+12m+8ЃЌ
ЃН80+4m2+12m+8ЃЌ
ећРэЕУЃК32m+32Љ16![]() ЃН0ЃЎ
ЃН0ЃЎ
ЩшaЃН![]() ЃЌдђга2a2ЉaЃН0ЃЌ
ЃЌдђга2a2ЉaЃН0ЃЌ
НтЕУЃКa3ЃН0ЃЈЩсШЅЃЉЃЌa4ЃН![]() ЃЌ
ЃЌ
ЁрmЃНЉ![]() ЃЌ
ЃЌ
ЁрЕуAЁфЕФзјБъЮЊ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃКдкЦНвЦЙ§ГЬжаЃЌЕБЁїAЁфBЁфCЪЧвдAЁфBЁфЮЊвЛЬѕжБНЧБпЕФжБНЧШ§НЧаЮЪБЃЌЕуAЁфЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
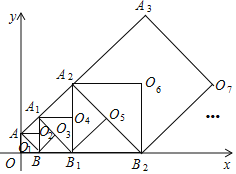
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮAOBO2ЕФЖЅЕуAЕФзјБъЮЊAЃЈ0ЃЌ2ЃЉЃЌO1ЮЊе§ЗНаЮAOBO2ЕФжааФЃЛвде§ЗНаЮAOBO2ЕФЖдНЧЯпABЮЊБпЃЌдкABЕФгвВрзїе§ЗНаЮABO3A1ЃЌO2ЮЊе§ЗНаЮABO3A1ЕФжааФЃЛдйвде§ЗНаЮABO3A1ЕФЖдНЧЯпA1BЮЊБпЃЌдкA1BЕФгвВрзїе§ЗНаЮA1BB1O4ЃЌO3ЮЊе§ЗНаЮA1BB1O4ЕФжааФЃЛдйвде§ЗНаЮA1BB1O4ЕФЖдНЧЯпA1B1ЮЊБпдкA1B1ЕФгвВрзїе§ЗНаЮA1B1O5A2ЃЌO4ЮЊе§ЗНаЮA1B1O5A2ЕФжааФЃКЁЃЛАДееДЫЙцТЩМЬајЯТШЅЃЌдђЕуO2018ЕФзјБъЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЕуAЃЈ0ЃЌ1ЃЉЁЂDЃЈ-2ЃЌ0ЃЉЃЌзїжБЯпADВЂвдЯпЖЮADЮЊвЛБпЯђЩЯзїе§ЗНаЮABCDЃЎ
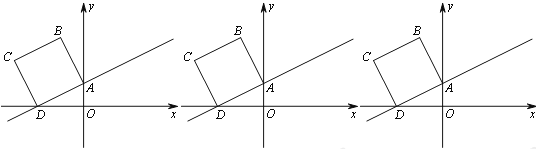
ЃЈ1ЃЉЬюПеЃКЕуBЕФзјБъЮЊ________ЃЌЕуCЕФзјБъЮЊ_________ЃЎ
ЃЈ2ЃЉШєе§ЗНаЮвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШбиЩфЯпDAЯђЩЯЦНвЦЃЌжБжСе§ЗНаЮЕФЖЅЕуCТфдкyжсЩЯЪБЭЃжЙдЫЖЏЃЎдкдЫЖЏЙ§ГЬжаЃЌЩше§ЗНаЮТфдкyжсгвВрВПЗжЕФУцЛ§ЮЊSЃЌЧѓSЙигкЦНвЦЪБМфtЃЈУыЃЉЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІЕФздБфСПtЕФШЁжЕЗЖЮЇЃЎ
ИіЕЅЮЛГЄЖШЕФЫйЖШбиЩфЯпDAЯђЩЯЦНвЦЃЌжБжСе§ЗНаЮЕФЖЅЕуCТфдкyжсЩЯЪБЭЃжЙдЫЖЏЃЎдкдЫЖЏЙ§ГЬжаЃЌЩше§ЗНаЮТфдкyжсгвВрВПЗжЕФУцЛ§ЮЊSЃЌЧѓSЙигкЦНвЦЪБМфtЃЈУыЃЉЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІЕФздБфСПtЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAЃЌBЮЊЖЈЕуЃЌЖЈжБЯпl//ABЃЌPЪЧlЩЯвЛЖЏЕуЃЎЕуMЃЌNЗжБ№ЮЊPAЃЌPBЕФжаЕуЃЌЖдгкЯТСаИїжЕЃК
ЂйЯпЖЮMNЕФГЄЃЛ
ЂкЁїPABЕФжмГЄЃЛ
ЂлЁїPMNЕФУцЛ§ЃЛ
ЂмжБЯпMNЃЌABжЎМфЕФОрРыЃЛ
ЂнЁЯAPBЕФДѓаЁЃЎ
ЦфжаЛсЫцЕуPЕФвЦЖЏЖјБфЛЏЕФЪЧЃЈ ЃЉ

A. ЂкЂл B. ЂкЂн C. ЂйЂлЂм D. ЂмЂн
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЖўДЮКЏЪ§y=ax2+bx+cЃЈaЃЌbЃЌcЪЧГЃЪ§ЃЌaЁй0ЃЉЭМЯѓЕФвЛВПЗжЃЌгыxжсЕФНЛЕуAдкЕуЃЈ2ЃЌ0ЃЉКЭЃЈ3ЃЌ0ЃЉжЎМфЃЌЖдГЦжсЪЧx=1ЃЎЖдгкЯТСаЫЕЗЈЃКЂйabЃМ0ЃЛЂк2a+b=0ЃЛЂл3a+cЃО0ЃЛЂмa+bЁнmЃЈam+bЃЉЃЈmЮЊЪЕЪ§ЃЉЃЛЂнЕБЉ1ЃМxЃМ3ЪБЃЌyЃО0ЃЌЦфжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ

A. ЂйЂкЂм B. ЂйЂкЂн C. ЂкЂлЂм D. ЂлЂмЂн
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
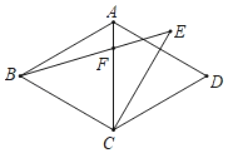
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌЁЯBADЃН120ЁуЃЌCEЁЭADЃЌЧвCEЃНBCЃЌСЌНгBEНЛЖдНЧЯпACгкЕуFЃЌдђЁЯEFCЃН_____ЁуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
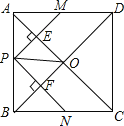
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЕуPЪЧABЩЯвЛЖЏЕуЃЈВЛгыAЃЌBжиКЯЃЉЃЌЖдНЧЯпACЃЌBDЯрНЛгкЕуOЃЌЙ§ЕуPЗжБ№зїACЃЌBDЕФДЙЯпЃЌЗжБ№НЛACЃЌBDгкЕуEЃЌFЃЌНЛADЃЌBCгкЕуMЃЌNЃЎЯТСаНсТлЃК
ЂйЁїAPEЁеЁїAMEЃЛЂкPM+PN=ACЃЛЂлPE2+PF2=PO2ЃЛЂмЁїPOFЁзЁїBNFЃЛЂнЕБЁїPMNЁзЁїAMPЪБЃЌЕуPЪЧABЕФжаЕуЃЎ
Цфжае§ШЗЕФНсТлга
AЃЎ5Иі BЃЎ4Иі CЃЎ3Иі DЃЎ2Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
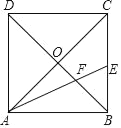
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ![]() +1ЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌAEЦНЗжЁЯBACЗжБ№НЛBCЁЂBDгкEЁЂFЃЌ
+1ЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌAEЦНЗжЁЯBACЗжБ№НЛBCЁЂBDгкEЁЂFЃЌ
ЃЈ1ЃЉЧѓжЄЃКЁїABFЁзЁїACEЃЛ
ЃЈ2ЃЉЧѓtanЁЯBAEЕФжЕЃЛ
ЃЈ3ЃЉдкЯпЖЮACЩЯеввЛЕуPЃЌЪЙЕУPE+PFзюаЁЃЌЧѓГізюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
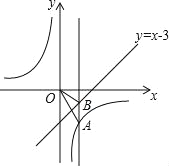
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAдкЗДБШКЏЪ§yЃН![]() ЃЈkЃМ0ЃЉЕФЭМЯѓЩЯЃЌЕуBдкжБЯпyЃНxЉ3ЕФЭМЯѓЩЯЃЌЕуBЕФзнзјБъЮЊЉ1ЃЌABЁЭxжсЃЌЧвSЁїOABЃН4ЃЎ
ЃЈkЃМ0ЃЉЕФЭМЯѓЩЯЃЌЕуBдкжБЯпyЃНxЉ3ЕФЭМЯѓЩЯЃЌЕуBЕФзнзјБъЮЊЉ1ЃЌABЁЭxжсЃЌЧвSЁїOABЃН4ЃЎ
ЃЈ1ЃЉЧѓЕуAЕФзјБъКЭkЕФжЕЃЛ
ЃЈ2ЃЉШєЕуPдкЗДБШР§КЏЪ§yЃН![]() ЃЈkЃМ0ЃЉЕФЭМЯѓЩЯЃЌЕуQдкжБЯпyЃНxЉ3ЕФЭМЯѓЩЯЃЌPЁЂQСНЕуЙигкyжсЖдГЦЃЌЩшЕуPЕФзјБъЮЊЃЈmЃЌnЃЉЃЌЧѓ
ЃЈkЃМ0ЃЉЕФЭМЯѓЩЯЃЌЕуQдкжБЯпyЃНxЉ3ЕФЭМЯѓЩЯЃЌPЁЂQСНЕуЙигкyжсЖдГЦЃЌЩшЕуPЕФзјБъЮЊЃЈmЃЌnЃЉЃЌЧѓ![]() +
+![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com