
【题目】已知,直线![]() ,点
,点![]() 为平面上一点,连接
为平面上一点,连接![]() 与
与![]() .
.
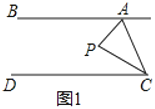
(1)如图1,点![]() 在直线
在直线![]() 、
、![]() 之间,当
之间,当![]() ,
,![]() 时,求
时,求![]() .
.
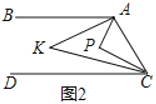
(2)如图2,点![]() 在直线
在直线![]() 、
、![]() 之间
之间![]() 左侧,
左侧,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,写出
,写出![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
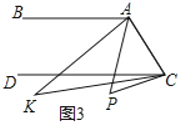
(3)如图3,点![]() 落在
落在![]() 下方,
下方,![]() 与
与![]() 的角平分线相交于点
的角平分线相交于点![]() ,
,![]() 与
与![]() 有何数量关系?并说明理由.
有何数量关系?并说明理由.
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如果两个角之差的绝对值等于60°,则称这两个角互为“互优角”,(本题中所有角都是指大于0°且小于180°的角).
(1)若∠1和∠2互为“互优角”,当∠1=90°时,则∠2=_____°;
(2)如图1,将一长方形纸片沿着EP对折(点P在线段BC上,点E在线段AB上)使点B落在点若与互为“互优角”,求∠BPE的度数;
(3)再将纸片沿着PF对折(点F在线段CD或AD上)使点C落在C′:
①如图2,若点E、C′、P在同一直线上,且![]() 与
与![]() 互为“互优角”,求∠EPF的度数(对折时,线段落在∠EPF内部);
互为“互优角”,求∠EPF的度数(对折时,线段落在∠EPF内部);
②若∠B′PC′与∠EPF互为“互优角”,则∠BPE求∠CPF应满足什么样的数量关系(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.
(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+4(k≠0)与x轴、y轴分别交于点B,A,直线y=-2x+1与y轴交于点C,与直线y=kx+4交于点D,△ACD的面积是![]() .
.
(1)求直线AB的表达式;
(2)设点E在直线AB上,当△ACE是直角三角形时,请直接写出点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,AC=FC.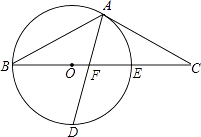
(1)求证:AC是⊙O的切线;
(2)已知圆的半径R=5,EF=3,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有15张大小、形状及背面完全相同的卡片,卡片正面分别画有正三角形、正方形、圆,从这15张卡片中任意抽取一张正面的图形既是轴对称图形,又是中心对称图形的概率是 ![]() ,则正面画有正三角形的卡片张数为( )
,则正面画有正三角形的卡片张数为( )
A.3
B.5
C.10
D.15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在某商店购买商品A,B共3次,只有一次购买时,商品同时打折,其余两次均按标价购买,三次购买商品A,B的数量和费用如下表:
购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
第一次购买 | 7 | 6 | 1350 |
第二次购买 | 4 | 8 | 1320 |
第三次购买 | 10 | 9 | 1188 |
(1)小明以折扣价购买商品的是第_____次购物;
(2)求商品A,B的标价;
(3)若商品A,B的折扣相同,问商店是打几折出售的这两种商品.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com