
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,⊙O的半径为3,![]() 的长为π.
的长为π.

(1)直线CD与⊙O相切吗?说明理由。
(2)求阴影部分的面积.
【答案】(1)、相切;理由见解析;(2)、![]()
【解析】
试题分析:(1)、连接OC,根据弧长的计算公式求出∠BOC的度数,根据等腰三角形的性质分别求出∠A和∠D的度数,然后根据三角形内角和定理得出∠OCD的度数,得出切线;(2)、作CH⊥OB于H,根据Rt△OCH求出CH的长度,然后根据阴影部分的面积=扇形OAC的面积-△OAC的面积得出答案.
试题解析:(1)、相切 连接OC,设∠BOC的度数为n° 则![]() =π 解得n=60°
=π 解得n=60°
∴∠A=![]() ∠BOC=30° ∵AC=CD,∴∠A=∠D=30°
∠BOC=30° ∵AC=CD,∴∠A=∠D=30°
∴∠OCD=180°-∠BOC-∠D=180°-30°﹣60°=90° ∴OC⊥CD ∴CD是⊙O的切线
(2)、作CH⊥OB于H,

则CH=OC![]() sin60°=3×
sin60°=3×![]() =
=![]() , ∵∠BOC=60°,∴∠AOC=120°,
, ∵∠BOC=60°,∴∠AOC=120°,
∴S阴影=S扇形OAC﹣S△OAC=![]() ﹣
﹣![]() ×3×
×3×![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)

查看答案和解析>>
科目:初中数学 来源: 题型:
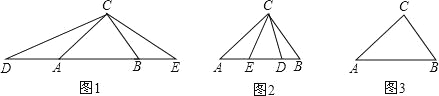
【题目】(1)如图(1),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在线段BA、AB的延长线上,且AD=AC,BE=BC,则∠DCE= ;
(2)如图(2),在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在边AB上,且AD=AC,BE=BC,求∠DCE的度数;
(3)在△ABC中,AB>AC>BC,∠ACB=80°,点D、E分别在直线AB上,且AD=AC,BE=BC,则∠求DCE的度数(直接写出答案);
(4)如图(3),在△ABC中,AB=14,AC=15,BC=13,点D、E在直线AB上,且AD=AC,BE=BC.请根据题意把图形补画完整,并在图形的下方直接写出△DCE的面积.(如果有多种情况,图形不够用请自己画出,各种情况用一个图形单独表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将点A(1,3)向左平移2个单位,再向下平移4个单位得到B,则点B的坐标为( )
A. (-2,-1) B. (-1,0) C. (-1,-1) D. (-2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则DF的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com