
已知,抛物线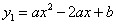 经过A(-1,0),C(2,
经过A(-1,0),C(2,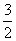 )两点,
)两点,
与x轴交于另一点B.
(1)求此抛物线的解析式;
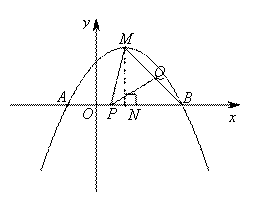
(2)若抛物线的顶点为M,点P为线段OB上一动点 (不与点B重合),点Q在线段MB上移动,且∠MPQ=45°,设线段OP=x,MQ= ,求y2与x的函数关系式,
,求y2与x的函数关系式,
并直接写出自变量x的取值范围.
 |
解:(1) ∵拋物线y1=ax2-2ax+b经过A(-1,0),C(0,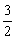 )两点,
)两点,
∴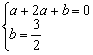 ,∴
,∴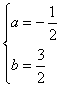 ,∴拋物线的解析式为y1= -
,∴拋物线的解析式为y1= -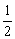 x2+x+
x2+x+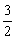
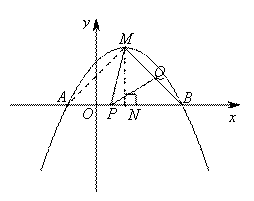
(2)解法一:过点M作MN⊥AB交AB于点N,连接AM
 由y1= -
由y1= -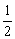 x2+x+
x2+x+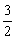 可知顶点M(1,2) ,A(-1,0),B(3,0),N(1,0)
可知顶点M(1,2) ,A(-1,0),B(3,0),N(1,0)
∴AB=4,MN=BN=AN=2,AM=MB=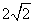 .
.
∴△AMN和△BMN为等腰直角三角形.
∵∠MPA+∠QPB=∠MPA +∠PMA=135°
∴∠QPB=∠PMA
又∵∠QBP=∠PAM=45°∴△QPB∽△PMA
∴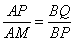 将AM=
将AM=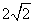 ,AP=x+1,BP=3-x,BQ=
,AP=x+1,BP=3-x,BQ= 代入,
代入,
 可得
可得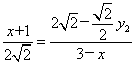 ,即
,即 .
.
∵点P为线段OB上一动点 (不与点B重合)∴0£x<3
则y2与x的函数关系式为y2=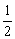 x2-x+
x2-x+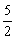 (0£x<3)
(0£x<3)
解法二:
过点M作MN⊥AB交AB于点N.
由y1= -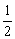 x2+x+
x2+x+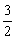 易得M(1,2),N(1,0),A(-1,0),B(3,0),
易得M(1,2),N(1,0),A(-1,0),B(3,0),
∴AB=4,MN=BN=2,MB=2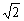 ,ÐMBN=45°
,ÐMBN=45°
根据勾股定理有BM 2-BN 2=PM 2-PN 2. ∴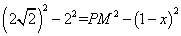 …①,
…①,
又ÐMPQ=45°=ÐMBP,∴△MPQ∽△MBP,∴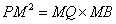 =
=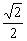 y2´2
y2´2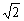
由j、k得y2=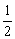 x2-x+
x2-x+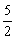 .
.
∵0£x<3,∴y2与x的函数关系式为y2=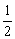 x2-x+
x2-x+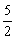 (0£x<3)
(0£x<3)


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
到2013底,我县已建立了比较完善的经济困难学生资助体系.某校2011年发放给每个经济困难学生450元,2013年发放的金额为625元.设每年发放的资助金额的平均增长率为x,则下面列出的方程中正确的是
A.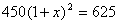 B.
B.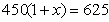
C.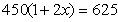 D.
D.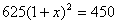
查看答案和解析>>
科目:初中数学 来源: 题型:
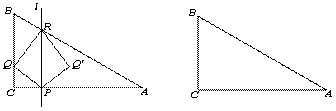
如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,点P、Q同时从点C出发,以1cm/s的速度分别沿CA、CB匀速运动,当点Q到达点B时,点P、Q同时停止运动.过点P作AC的垂线l交AB于点R,连接PQ、RQ,并作△PQR关于直线l对称的图形,得到△PQ'R.设点Q的运动时间为t(s),△PQ'R与△PAR重叠部分的面积为S(cm2).
(1)t为何值时,点Q' 恰好落在AB上?
(2)求S与t的函数关系式,并写出t的取值范围.
(3)S能否为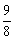 ?若能,求出此时t的值;若不能,请说明理由.
?若能,求出此时t的值;若不能,请说明理由.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
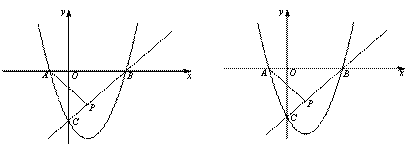
已知抛物线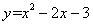 经过A、B、C三点,点P(1,k)在直线BC:y=x
经过A、B、C三点,点P(1,k)在直线BC:y=x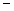 3上,若点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的四边形为平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.
3上,若点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的四边形为平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
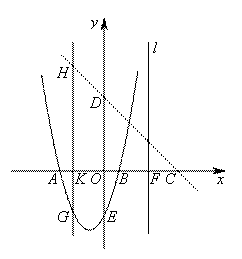
如图,抛物线y=ax2+bx+c交x轴于点A(-3,0),点B(1,0),交y轴于点E(0,-3).点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于点D.
(1)求抛物线的解析式;
(2)点K为线段AB上一动点,过点K作x轴的垂线,交直线CD于点H,交抛物线于点G,求线段HG长度的最大值;
(3)在直线l上取点M,在抛物线上取点N,使以A,C,M,N为顶点的四边形是平行四边形,求点N的坐标.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读理解:配方法是中学数学的重要方法,用配方法可求最大(小)值。
对于任意正实数a、b,可作如下变形a+b=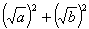 =
=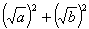 -
- +
+ =
= +
+  ,
,
又∵ ≥0, ∴
≥0, ∴ +
+  ≥0+
≥0+ ,即
,即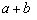 ≥
≥ .
.
(1)根据上述内容,回答下列问题:在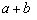 ≥
≥ (a、b均为正实数)中,若ab为定值p,则a+b≥
(a、b均为正实数)中,若ab为定值p,则a+b≥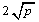 ,当且仅当a、b满足 时,a+b有最小值
,当且仅当a、b满足 时,a+b有最小值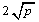 .
.
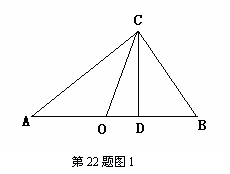
(2)思考验证:如图1,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,CO为AB边上中线,AD=2a,DB=2b, 试根据图形验证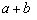 ≥
≥ 成立,并指出等号成立时的条件.
成立,并指出等号成立时的条件.
 (3)探索应用:如图2,已知A为反比例函数
(3)探索应用:如图2,已知A为反比例函数 的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.
的图像上一点,A点的横坐标为1,将一块三角板的直角顶点放在A处旋转,保持两直角边始终与x轴交于两点D、E,F(0,-3)为y轴上一点,连结DF、EF,求四边形ADFE面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知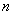 是正整数,则奇数可以用代数式
是正整数,则奇数可以用代数式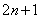 来表示.
来表示.
(1)分解因式: 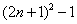 ;
;
(2)我们把所有”奇数的平方减去1”所得的数叫”白银数”,则所有”白银数”的最大公约数是多少?请简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com