
【题目】如图,在△ABC中,AB=AC=2 ![]() ,∠BAC=120°,点D,E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为 .
,∠BAC=120°,点D,E都在边BC上,∠DAE=60°.若BD=2CE,则DE的长为 . 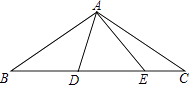
【答案】3 ![]() ﹣3
﹣3
【解析】(方法一)将△ABD绕点A逆时针旋转120°得到△ACF,连接EF,过点E作EM⊥CF于点M,过点A作AN⊥BC于点N,如图所示.
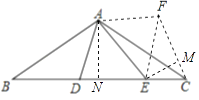
∵AB=AC=2 ![]() ,∠BAC=120°,
,∠BAC=120°,
∴BN=CN,∠B=∠ACB=30°.
在Rt△BAN中,∠B=30°,AB=2 ![]() ,
,
∴AN= ![]() AB=
AB= ![]() ,BN=
,BN= ![]() =3,
=3,
∴BC=6.
∵∠BAC=120°,∠DAE=60°,
∴∠BAD+∠CAE=60°,
∴∠FAE=∠FAC+∠CAE=∠BAD+∠CAE=60°.
在△ADE和△AFE中, 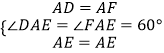 ,
,
∴△ADE≌△AFE(SAS),
∴DE=FE.
∵BD=2CE,BD=CF,∠ACF=∠B=30°,
∴设CE=2x,则CM=x,EM= ![]() x,FM=4x﹣x=3x,EF=ED=6﹣6x.
x,FM=4x﹣x=3x,EF=ED=6﹣6x.
在Rt△EFM中,FE=6﹣6x,FM=3x,EM= ![]() x,
x,
∴EF2=FM2+EM2,即(6﹣6x)2=(3x)2+( ![]() x)2,
x)2,
解得:x1= ![]() ,x2=
,x2= ![]() (不合题意,舍去),
(不合题意,舍去),
∴DE=6﹣6x=3 ![]() ﹣3.
﹣3.
所以答案是:3 ![]() ﹣3.
﹣3.
(方法二):将△ABD绕点A逆时针旋转120°得到△ACF,取CF的中点G,连接EF、EG,如图所示.
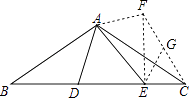
∵AB=AC=2 ![]() ,∠BAC=120°,
,∠BAC=120°,
∴∠ACB=∠B=∠ACF=30°,
∴∠ECG=60°.
∵CF=BD=2CE,
∴CG=CE,
∴△CEG为等边三角形,
∴EG=CG=FG,
∴∠EFG=∠FEG= ![]() ∠CGE=30°,
∠CGE=30°,
∴△CEF为直角三角形.
∵∠BAC=120°,∠DAE=60°,
∴∠BAD+∠CAE=60°,
∴∠FAE=∠FAC+∠CAE=∠BAD+∠CAE=60°.
在△ADE和△AFE中, 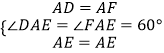 ,
,
∴△ADE≌△AFE(SAS),
∴DE=FE.
设EC=x,则BD=CD=2x,DE=FE=6﹣3x,
在Rt△CEF中,∠CEF=90°,CF=2x,EC=x,
EF= ![]() =
= ![]() x,
x,
∴6﹣3x= ![]() x,
x,
x=3﹣ ![]() ,
,
∴DE= ![]() x=3
x=3 ![]() ﹣3.
﹣3.
所以答案是:3 ![]() ﹣3.
﹣3.
【考点精析】通过灵活运用勾股定理的概念和旋转的性质,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了即可以解答此题.


科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,高新区凌水河治理工程正式启动,若由甲工程队单独完成需10个月;若由甲、乙两工程队合做4个月后,剩下工程由乙工程队再做5个月可以完成。(1)乙工程队单独完成这项工程需几个月的时间?
(2)已知甲工程队每月施工费用为15万元,比乙工程队多6万元,按要求该工程总费用不超过141万元,工程必须在一年内竣工(包括12个月).为了确保经费和工期,采取甲、乙工程队同时开工,甲工程队做![]() 个月,乙工程队做
个月,乙工程队做![]() 个月(
个月(![]() 均为整数)分工合作的方式施工,问有哪几种施工方案?
均为整数)分工合作的方式施工,问有哪几种施工方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,各内角的平分线分别相交于点E,F,G,H.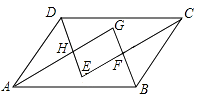
(1)求证:△ABG≌△CDE;
(2)猜一猜:四边形EFGH是什么样的特殊四边形?证明你的猜想;
(3)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于两点A(﹣4,0)和B(1,0),与y轴交于点C(0,2),动点D沿△ABC的边AB以每秒2个单位长度的速度由起点A向终点B运动,过点D作x轴的垂线,交△ABC的另一边于点E,将△ADE沿DE折叠,使点A落在点F处,设点D的运动时间为t秒.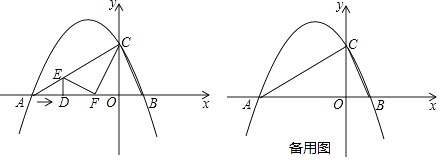
(1)求抛物线的解析式和对称轴;
(2)是否存在某一时刻t,使得△EFC为直角三角形?若存在,求出t的值;若不存在,请说明理由;
(3)设四边形DECO的面积为s,求s关于t的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校“百变魔方”社团准备购买![]() ,
,![]() 两种魔方.已知购买2个
两种魔方.已知购买2个![]() 种魔方和6个
种魔方和6个![]() 种魔方共需130元,购买3个
种魔方共需130元,购买3个![]() 种魔方和4个
种魔方和4个![]() 种魔方所需款数相同.
种魔方所需款数相同.
(1)求这两种魔方的单价;
(2)结合社员们的需求,社团决定购买![]() ,
,![]() 两种魔方共100个(其中
两种魔方共100个(其中![]() 种魔方不超过50个).某商店有两种优惠活动,如图所示.
种魔方不超过50个).某商店有两种优惠活动,如图所示.
请根据以上信息,说明选择哪种优惠活动购买魔方更实惠.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们知道:“在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.”
(1)请写出它的逆命题 ;该逆命题是一个 命题(填“真”或“假”)
(2)若你的判断是真命题请写出证明过程(要求画图,并写出已知,求证).若是假命题,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
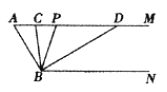
【题目】如图,已知AM//BN,∠A=600.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)①∠ABN的度数是 ;②∵AM //BN,∴∠ACB=∠ ;
(2)求∠CBD的度数;
(3)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(4)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC⊥x轴于点A,点B在y轴的正半轴上,∠ABC=60°,AB=4,BC=2 ![]() ,点D为AC与反比例函数y=
,点D为AC与反比例函数y= ![]() 的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为 .
的图象的交点.若直线BD将△ABC的面积分成1:2的两部分,则k的值为 . 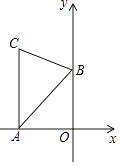
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com