
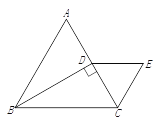
【题目】如图,△ABC为等边三角形,过点B作BD⊥AC于点D,过D作DE∥BC,且DE=CD,连接CE,
(1)求证:△CDE为等边三角形;
(2)请连接BE,若AB=4,求BE的长.
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)由△ABC为等边三角形得∠ACB=60°,又DE∥BC知∠EDC=60°,且DE=DC,从而可证△CDE为等边三角形;
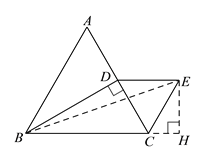
(2)过点E作EH⊥BC于H,求出EH和CH的长,利用勾股定理即可求出BE的长.
试题解析:(1)∵△ABC为等边三角形
∴∠ACB=60°
∵DE∥BC
∴∠EDC=∠ACB=60°
又∵DE=DC
∴△CDE为等边三角形
(2)过点E作EH⊥BC于H
∵BD⊥AC ∴CD=![]() AC=
AC=![]() AB=2
AB=2
又∵△CDE为等边三角形
∴CE=CD=2
∵∠ECH=60°
∴EH=EC·sin60°=2×![]() =
=![]() ,CH=EC·cos60°=1
,CH=EC·cos60°=1
∴![]()


科目:初中数学 来源: 题型:
【题目】学校准备设计一款女生校服,对全校女生喜欢的颜色进行了问卷调查,统计如下表所示:
颜色 | 黄色 | 绿色 | 白色 | 紫色 | 红色 |
学生人数 | 100 | 180 | 220 | 80 | 750 |
学校决定采用红色,可用来解释这一现象的统计知识是( )
A. 平均 B. 中位数 C. 众数 D. 方差
查看答案和解析>>
科目:初中数学 来源: 题型:
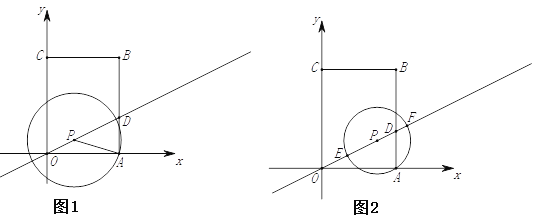
【题目】如图1,直角坐标系中有一矩形OABC,其中O是坐标原点,点A,C分别在x轴和y轴上,点B的坐标为(3,4),直线![]() 交AB于点D,点P是直线
交AB于点D,点P是直线![]() 位于第一象限上的一点,连接PA,以PA为半径作⊙P,
位于第一象限上的一点,连接PA,以PA为半径作⊙P,
(1)连接AC,当点P落在AC上时, 求PA的长;
(2)当⊙P经过点O时,求证:△PAD是等腰三角形;
(3)设点P的横坐标为m,
①在点P移动的过程中,当⊙P与矩形OABC某一边的交点恰为该边的中点时,求所有满足要求的m值;
②如图2,记⊙P与直线![]() 的两个交点分别为E,F(点E在点P左下方),当DE,DF满足
的两个交点分别为E,F(点E在点P左下方),当DE,DF满足![]() 时,求m的取值范围.(请直接写出答案)
时,求m的取值范围.(请直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com