
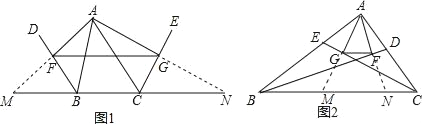
【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得: ![]() 的值为常数t,则t= .
的值为常数t,则t= . 
【答案】
(1)证明:①∵四边形ABCD是平行四边形,∠BAD=120°,
∴∠D=∠B=60°,
∵AD=AB,
∴△ABC,△ACD都是等边三角形,
∴∠B=∠CAD=60°,∠ACB=60°,BC=AC,
∵∠ECF=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=60°,
∴∠BCE=∠ACF,
在△BCE和△ACF中,
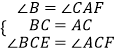
∴△BCE≌△ACF.
②∵△BCE≌△ACF,
∴BE=AF,
∴AE+AF=AE+BE=AB=AC.
(2)证明:设DH=x,由题意,CD=2x,CH= ![]() x,
x,
∴AD=2AB=4x,
∴AH=AD﹣DH=3x,
∵CH⊥AD,
∴AC= ![]() =2
=2 ![]() x,
x,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴∠BAC=∠ACD=90°,
∴∠CAD=30°,
∴∠ACH=60°,
∵∠ECF=60°,
∴∠HCF=∠ACE,
∴△ACE∽△HCF,
∴ ![]() =
= ![]() =2,
=2,
∴AE=2FH.
(3)![]()
【解析】解; (3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.
∵∠ECF+∠EAF=180°,
∴∠AEC+∠AFC=180°,
∵∠AFC+∠CFN=180°,
∴∠CFN=∠AEC,∵∠M=∠CNF=90°,
∴△CFN∽△CEM,
∴ ![]() =
= ![]() ,
,
∵ABCM=ADCN,AD=3AB,
∴CM=3CN,
∴ ![]() =
= ![]() =
= ![]() ,设CN=a,FN=b,则CM=3a,EM=3b,
,设CN=a,FN=b,则CM=3a,EM=3b,
∵∠MAH=60°,∠M=90°,
∴∠AHM=∠CHN=30°,
∴HC=2a,HM=a,HN= ![]() a,
a,
∴AM= ![]() a,AH=
a,AH= ![]() a,
a,
∴AC= ![]() =
= ![]() a,
a,
AE+3AF=(EM﹣AM)+3(AH+HN﹣FN)=EM﹣AM+3AH+3HN﹣3FN=3AH+3HN﹣AM= ![]() a,
a,
∴ ![]() =
= ![]() =
= ![]() .
.
故答案为 ![]() .
.
(1)①先证明△ABC,△ACD都是等边三角形,再证明∠BCE=∠ACF即可解决问题.②根据①的结论得到BE=AF,由此即可证明.(2)设DH=x,由题意,CD=2x,CH= ![]() x,由△ACE∽△HCF,得
x,由△ACE∽△HCF,得 ![]() =
= ![]() 由此即可证明.(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.先证明△CFN∽△CEM,得
由此即可证明.(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.先证明△CFN∽△CEM,得 ![]() =
= ![]() ,由ABCM=ADCN,AD=3AB,推出CM=3CN,所以
,由ABCM=ADCN,AD=3AB,推出CM=3CN,所以 ![]() =
= ![]() =
= ![]() ,设CN=a,FN=b,则CM=3a,EM=3b,想办法求出AC,AE+3AF即可解决问题.
,设CN=a,FN=b,则CM=3a,EM=3b,想办法求出AC,AE+3AF即可解决问题.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=108°.
(1)实践与操作:作AB的垂直平分线DE,与AB,BC分别交于点D,E(用尺规作图.保留作图痕迹,不要求写作法)
(2)推理与计算:求∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到对应点C,D,连接AC,BD.
(1)求出点C,D的坐标;
(2)设y轴上一点P(0,m),m为整数,使关于x,y的二元一次方程组![]() 有正整数解,求点P的坐标;
有正整数解,求点P的坐标;
(3)在(2)的条件下,若Q点在线段CD上,横坐标为n,△PBQ的面积S△PBQ的值不小于0.6且不大于4,求n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年北京奥运会后,同学们参与体育锻炼的热情高涨.为了解他们平均每周的锻炼时间,小明同学在校内随机调查了50名同学,统计并制作了如下的频数分布表和扇形统计图.根据上述信息解答下列问题: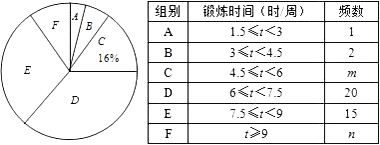
(1)m= , n=;
(2)在扇形统计图中,D组所占圆心角的度数为度;
(3)全校共有3000名学生,估计该校平均每周体育锻炼时间不少于6小时的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】几何证明:
(1)已知:如图1,BD、CE分别是△ABC的外角平分线,过点A作AF⊥BD,AG⊥CE,垂足分别是F、G,连接FG,延长AF、AG,与直线BC相交.求证:FG=![]() (AB+BC+AC).
(AB+BC+AC).
(2)若BD、CE分别是△ABC的内角平分线,其余条件不变(如图1),线段FG与△ABC的三边又有怎样的数量关系?写出你的猜想,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
求证:AF平分∠BAC.

【答案】证明见解析.
【解析】试题分析:先根据AB=AC,可得∠ABC=∠ACB,再由垂直,可得90°的角,在△BCE和△BCD中,利用内角和为180°,可分别求∠BCE和∠DBC,利用等量减等量差相等,可得FB=FC,再易证△ABF≌△ACF,从而证出AF平分∠BAC.
试题解析:证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高,
∴BD⊥AC,CE⊥AB(高的定义).
∴∠CEB=∠BDC=90°.
∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.
∴∠ECB=∠DBC(等量代换).
∴FB=FC(等角对等边),
在△ABF和△ACF中,
 ,
,
∴△ABF≌△ACF(SSS),
∴∠BAF=∠CAF(全等三角形对应角相等),
∴AF平分∠BAC.
【题型】解答题
【结束】
23
【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.

(1)求证:CD=BE;
(2)已知CD=2,求AC的长;
(3)求证:AB=AC+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于“倍根方程”的说法:①方程x2-3x+2=0是“倍根方程”;②若(x-2)(mx+n)=0是“倍根方程”,则4m2+5mn+n2=0;③若pq=2,则关于x的方程px2+3x+q=0是“倍根方程”;④若方程ax2+bx+c=0是“倍根方程”,且5a+b=0,则方程ax2+bx+c=0的一个根为![]() .其中正确的是____(填序号).
.其中正确的是____(填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB<BC.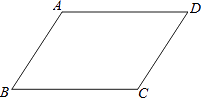
(1)利用尺规作图,在AD边上确定点E,使点E到边AB,BC的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则DE= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com