
【题目】函数y1=kx2+ax+a的图象与x轴交于点A,B(点A在点B的左侧),函数y2=kx2+bx+b,的图象与x轴交于点C,D(点C在点D的左侧),其中k≠0,a≠b.
(1)求证:函数y1与y2的图象交点落在一条定直线上;
(2)若AB=CD,求a,b和k应满足的关系式;
(3)是否存在函数y1和y2,使得B,C为线段AD的三等分点?若存在,求![]() 的值,若不存在,说明理由
的值,若不存在,说明理由
【答案】(1) 见解析;(2) a+b=4k ;(3) ![]() =
=![]() 或
或![]()
【解析】
(1)使两个函数关系式相等,根据已知求出x的值即可判断;
(2)表示出A、B、C、D的坐标,求出AB、CD,列方程求解即可;
(3)方法与(2)相同,利用三等分点条件,列方程求解即可.
(1)当y1=y2时,kx2+ax+a=kx2+bx+b,
∵a≠b,
∴x=﹣1,
∴函数y1与y2的图象交点落在一条定直线上;
(2)若AB=CD则xB﹣xA=xD﹣xC,
A、B、C、D为抛物线与x轴的交点,可得
xA=![]() ,xB=
,xB=![]() ,
,
xC=![]() ,xD=
,xD=![]() ,
,
代入xB﹣xA=xD﹣xC得
![]() -
-![]() =
=![]() -
-![]() ,
,
所以a+b=4k;
(3)因为B、C为线段AD的三等分点,
当点B在点C左侧时,BC=CD,则有xC﹣xD=xC﹣xB,
∴2xC=xD+xB,
∴2×![]() =
=![]() +
+![]() ,
,
整理得:a2+b2+14ab=0,
∴(![]() )2+
)2+![]() +1=0,
+1=0,
解得![]() =
=![]() 或
或![]() ;
;
当点C在点B左侧时,AC=BC,则有xC﹣xA=xB﹣xC,
∴2xC=xA+xB,
∴2×![]() =
=![]() +
+![]() ,
,
即![]() =
=![]() ,
,
整理得:a-b=![]() ,
,
∵a+b=4k,
∴a-b=![]() ,
,
即a-b=![]() ,
,
a2+b2-ab=0,
∴(![]() )2-
)2-![]() +1=0,
+1=0,
△<0,方程无解,
综上,![]() 的值为
的值为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
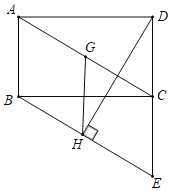
【题目】如图,矩形ABCD,过点B作BE∥AC交DC的延长线于点E.过点D作DH⊥BE于H,G为AC中点,连接GH.
(1)求证:BE=AC.
(2)判断GH与BE的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.

请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?
(2)请将条形统计图补充完整;
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
(4)该校广播站需要广播员,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E是CD边上的点,过点E作EF⊥BD于F.
(1)尺规作图:在图中求作点E,使得EF=EC;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接FC,求∠BCF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
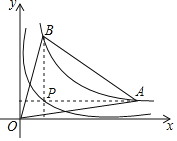
【题目】如图,点P为函数y=![]() (x>0)图象上一点,过点P作x轴、y轴的平行线,分别与函数y=
(x>0)图象上一点,过点P作x轴、y轴的平行线,分别与函数y=![]() (x>0)的图象交于点A、B,则△AOB的面积为_____.
(x>0)的图象交于点A、B,则△AOB的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校七年级学生每周上网的时间,甲、乙两名学生进行了抽样调查.甲同学调查了七年级电脑爱好者中40名学生每周上网的时间;乙同学从全校800名七年级学生中随机抽取了40名学生,调查了每周上网的时间.甲、乙同学各自整理的样本数据如表:
上网时间t(小时/周) | 甲学生抽样人数(人) | 乙学生抽样人数(人) |
0≤t<1.5 | 6 | 22 |
1.5≤t<2.5 | 10 | 10 |
2.5≤t<3.5 | 16 | 6 |
t≥3.5 | 8 | 2 |
(1)你认为哪名学生抽取的样本不合理,请说明理由.
(2)请你根据抽取样本合理的学生的数据,将调查结果绘制成合适的统计图(绘制一种即可).
(3)专家建议每周上网2.5小时以上(含2.5小时)的学生应适当减少上网的时间,估计该校全体七年级学生中应适当减少上网的时间的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
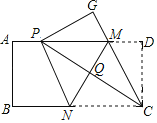
【题目】如图,先有一张矩形纸片![]() 点
点![]() 分别在矩形的边
分别在矩形的边![]() 上,将矩形纸片沿直线MN折叠,使点
上,将矩形纸片沿直线MN折叠,使点![]() 落在矩形的边
落在矩形的边![]() 上,记为点
上,记为点![]() ,点
,点![]() 落在
落在![]() 处,连接
处,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:
.下列结论:
![]()
②四边形![]() 是菱形;
是菱形;
③![]() 重合时,
重合时,![]() ;
;
④![]() 的面积
的面积![]() 的取值范围是
的取值范围是![]()
其中正确的是_____(把正确结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
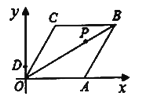
【题目】已知菱形![]() 在平面直角坐标系的位置如图所示,顶点
在平面直角坐标系的位置如图所示,顶点![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上的一个动点,
上的一个动点,![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上的一个动点,
上的一个动点,![]() ,当
,当![]() 最短时,点
最短时,点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com