
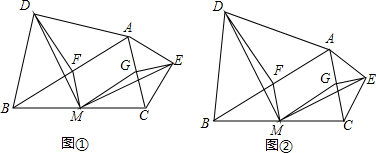
���� ��1�������������ε���λ�ߵ�����֤��FM��AC��MG��AB���Ӷ���֪�ı���AFMG����״��
��������ֱ��������б�������ߵ����ʺ�ƽ���ı��ε�����֤��DF=MG��FM=EG��Ȼ�����ݵ������������ߺ�һ�����ʺ�ƽ���ߵ�����֤����DFM=��EGM������SAS��֤������������ȫ�ȣ�
��2������֤����DFM=��MGE��Ȼ����֤����1=��3������������Ǻ����Ķ���ɵõ�$\frac{DF}{MG}=\frac{FM}{GE}$��������ݶ�Ӧ�߳ɱ����Ҽн���ȵ������������ƿ�֤����DFM�ס�MGE���������ݹ��ɶ������DF=4��Ȼ�����á�DFM���MGE�����Ʊȣ�Ȼ���������������ε�����ȵ������Ʊȵ�ƽ����⼴�ɣ�
��� �⣺��1���١�BF=AF��BM=MC��
��FM��AC��ͬ��MG��AB��
���ı���AFMG��ƽ���ı��Σ�
�ڡߡ�BDA=90�㣬DF��AB���ϵ����ߣ�
��DF=AF��
���ı���AFMG��ƽ���ı��Σ�
��MG=AF����AFM=��AGM��
��DF=MG����BFM=��MGC��
�ߡ�AEC=90�㣬EG��AC���ϵ����ߣ�
��GE=AG��
���ı���AFMG��ƽ���ı��Σ�
��AG=FM��
��GE=FM��
��DA=DB��FΪAB���е㣬
���DFB=90�㣮
ͬ������EGC=90�㣮
���DFB+��BFM=��EGC+��MGC������DFM=��EGM��
�ڡ�DFM�͡�MGE�У�
$\left\{\begin{array}{l}{DF=MG}\\{��DFM=��EGM}\\{FM=EG}\end{array}\right.$��
���DFM�ա�MGE��
�ʴ�Ϊ����ƽ���ı��Σ���ȫ�ȣ�
��2���١ߡ�ADB�͡�ACE���ǵ��������Σ���F��GΪAB��AC���е㣬
���DFB=��EGC=90�㣮
�ߵ�F��M��G�ֱ�ΪAB��BC��AC�ߵ��е㣬
��FM��AC��MG��AB��FM=$\frac{1}{2}$AC=AG��MG=$\frac{1}{2}$AB=AF��
���BFM=��BAC=��MGC��
���BFM+90��=��MGC+90�㣬����DFM=��MGE��
�ߡ�DAF+��CAE=90�㣬��GAE+��AEG=90�㣬
���DAF=��AEG��
��tan��DAF=tan��AEG��
��$\frac{DF}{AF}=\frac{AG}{GE}$����$\frac{DF}{MG}=\frac{FM}{GE}$��
�֡ߡ�DFM=��MGE��
���DFM�ס�MGE��
�ڡ�AD=5��AB=6��
��AF=3��MG=3��MG=AF=3��
����Rt��ADF��DF=$\sqrt{A{D}^{2}-A{F}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4��
���ɢ�֪��DFM�ס�MGE���ҡ�DFM�����Ϊ32��
��$\frac{{S}_{��MGE}}{{S}_{��DFM}}$=��$\frac{MG}{DF}$��2=��$\frac{3}{4}$��2=$\frac{9}{16}$��
��S��MGE=32��$\frac{9}{16}$=18��
���� ������Ҫ������������Ρ��ı��ε��ۺ�Ӧ�ã��������ҪӦ���������ε���λ�߶�����ƽ���ı��ε����ʺ��ж���ȫ�������ε����ʺ��ж������������ε����ʺ��ж������ɶ�����Ӧ�ã��ҳ���DFM���MGEȫ�Ȼ����Ƶ������ǽ���Ĺؼ���


 ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
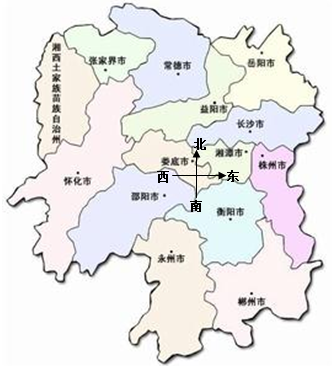
| A�� | ������λ��¦������ƫ��Լ35��ķ����� | |
| B�� | ������λ�������б�ƫ��Լ60��ķ����� | |
| C�� | ������λ��¦������ƫ��Լ 5��ķ����� | |
| D�� | ������λ�ڳ�ɳ�б�ƫ��Լ45��ķ����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{��-10��^{2}}$=10 | B�� | ��-2$\sqrt{2}$��2=8 | C�� | ��$\sqrt{-10}$��2=10 | D�� | -$\sqrt{��-\frac{3}{5}��^{2}}$=-$\frac{3}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
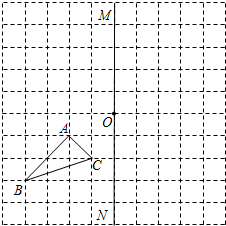 ����ͼ�������������У�ÿ��С�����εı߳����ǵ�λ1����ABC�Ķ�����ڸ���ϣ�
����ͼ�������������У�ÿ��С�����εı߳����ǵ�λ1����ABC�Ķ�����ڸ���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��\sqrt{0.36}$=��0.6 | B�� | $\sqrt{9}=��3$ | C�� | $\root{3}{��-3��^{3}}$=3 | D�� | $\sqrt{��-2��^{2}}$=-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | b��a��c | C�� | c��a��b | D�� | b��c��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2x3y��2=4x6y2 | B�� | $\sqrt{��-4������-9��}$=$\sqrt{-4}$��$\sqrt{-9}$ | C�� | a6��a3=a2 | D�� | a4+a2=a6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��4 | B�� | x��4 | C�� | x��4��x��2 | D�� | x��2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com