
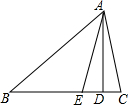
 如图,在△ABC中,∠ABC=42°,∠EAD=20°,AD是BC边上的高,AE平分∠BAC.
如图,在△ABC中,∠ABC=42°,∠EAD=20°,AD是BC边上的高,AE平分∠BAC.分析 (1)根据直角三角形两锐角互余求出∠AED,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAE,然后根据角平分线的定义求出∠BAC;
(2)再利用三角形的内角和定理列式计算即可得解.
解答 解:(1)∵AD是BC边上的高,∠EAD=20°,
∴∠AED=70°,
∵∠B=42°,
∴∠BAE=∠AED-∠B=70°-42°=28°,
∵AE是∠BAC的角平分线,
∴∠BAC=2∠BAE=56°,
(2)∵∠C=180°-∠B-∠BAC=180°-42°-56°=82°,
∴∠CAD=8°.
点评 本题考查了三角形的角平分线、中线和高,主要利用了直角三角形两锐角互余,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,熟记各性质并准确识图是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
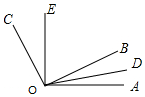 如图,OB在∠AOC内部,且∠BOC=3∠AOB,OD是∠AOB的平分线,∠BOC=3∠COE,则下列结论:①∠EOC=$\frac{1}{3}$∠AOE; ②∠DOE=5∠BOD; ③∠BOE=$\frac{1}{2}$(∠AOE+∠BOC);④∠AOE=$\frac{6}{5}$ (∠BOC-∠AOD).其中正确结论有①②④.
如图,OB在∠AOC内部,且∠BOC=3∠AOB,OD是∠AOB的平分线,∠BOC=3∠COE,则下列结论:①∠EOC=$\frac{1}{3}$∠AOE; ②∠DOE=5∠BOD; ③∠BOE=$\frac{1}{2}$(∠AOE+∠BOC);④∠AOE=$\frac{6}{5}$ (∠BOC-∠AOD).其中正确结论有①②④.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在平面直角坐标系中,B、C的坐标为(-10,0)、(-10,5),P、Q两点分别是x轴、y轴上的动点,且满足PQ=OC,问P、Q点运动到何处时,△OBC才能和以P、Q、O为顶点的三角形全等.
如图,已知在平面直角坐标系中,B、C的坐标为(-10,0)、(-10,5),P、Q两点分别是x轴、y轴上的动点,且满足PQ=OC,问P、Q点运动到何处时,△OBC才能和以P、Q、O为顶点的三角形全等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小强有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各题:
小强有5张写着不同数字的卡片,请你按要求抽出卡片,完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
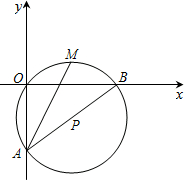 如图在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上,M为劣弧OB的中点.
如图在平面直角坐标系中,O(0,0),A(0,-6),B(8,0)三点在⊙P上,M为劣弧OB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com