
【题目】已知AB,CD都是![]() 的直径,连接DB,过点C的切线交DB的延长线于点E.
的直径,连接DB,过点C的切线交DB的延长线于点E.
![]() 如图1,求证:
如图1,求证:![]() ;
;
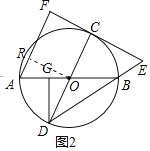
![]() 如图2,过点A作
如图2,过点A作![]() 交EC的延长线于点F,过点D作
交EC的延长线于点F,过点D作![]() ,垂足为点G,求证:
,垂足为点G,求证:![]() ;
;
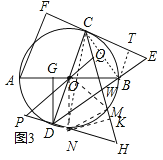
![]() 如图3,在
如图3,在![]() 的条件下,当
的条件下,当![]() 时,在
时,在![]() 外取一点H,连接CH、DH分别交
外取一点H,连接CH、DH分别交![]() 于点M、N,且
于点M、N,且![]() ,点P在HD的延长线上,连接PO并延长交CM于点Q,若
,点P在HD的延长线上,连接PO并延长交CM于点Q,若![]() ,
,![]() ,
,![]() ,求线段HM的长.
,求线段HM的长.

【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
(1)由∠D+∠E=90°,可得2∠D+2∠E=180°,只要证明∠AOD=2∠D即可;
(2)如图2中,作OR⊥AF于R.只要证明△AOR≌△ODG即可;
(3)如图3中,连接BC、OM、ON、CN,作BT⊥CL于T,作NK⊥CH于K,设CH交DE于W.解直角三角形分别求出KM,KH即可;
![]() 证明:如图1中,
证明:如图1中,
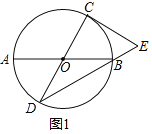
![]() 与CE相切于点C,
与CE相切于点C,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() 证明:如图2中,作
证明:如图2中,作![]() 于R.
于R.
![]() ,
,
![]() 四边形OCFR是矩形,
四边形OCFR是矩形,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() 解:如图3中,连接BC、OM、ON、CN,作
解:如图3中,连接BC、OM、ON、CN,作![]() 于T,作
于T,作![]() 于K,设CH交DE于W.
于K,设CH交DE于W.
设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为直径,
为直径,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 负根已经舍弃
负根已经舍弃![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等边三角形,
是等边三角形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的面积为1cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2016C2017B的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中, ∠C=90°,边AB的垂直平分线交AB、AC分别于点D,点E,连结BE.

(1)若∠A=40°,求∠CBE的度数.
(2)若AB=10,BC=6,求△BCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2017= ______ .
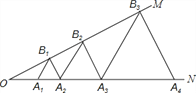
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=30°,点M,N分别在边OA,OB上,OM=5,ON=12,点P,Q分别在边OB,OA上运动,连接MP,PQ,QN,则MP+PQ+QN的最小值为 ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本的作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法.
我们有多少种剪法,图1是其中的一种方法:

定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=x°,试画出示意图,并求出x所有可能的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN,与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )

A. r B. ![]() r C. 2r D.
r C. 2r D. ![]() r
r
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,点M为AB延长线上的一点,MC与⊙O相切于点C,圆周上有另一点D与点C分居直径AB两侧,且使得MC=MD=AC,连接AD.现有下列结论:①MD与⊙O相切;②四边形ACMD是菱形;③AB=MO;④∠ADM=120°,其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com