
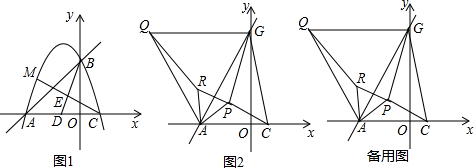
分析 (Ⅰ)抛物线y=-x2-2x+3中,令y=-x2-2x+3=0,可得A(-3,0),C(1,0);当x=0时,可得B(0,3);
(Ⅱ)首先利用A、C坐标,求出D的坐标,根据BE=2ED,求出点E坐标,求出直线CE,利用方程组求交点坐标M即可;
(Ⅲ)先证明△QAR≌△GAP即可得出QR=PG,进而得到PA+PC+PG=PR+PC+QR,可得当Q,R,P,C共线时,PA+PC+PG的值最小,即为线段QC的长,作QN⊥OA于N,AM⊥QC于M,PK⊥OA于K,利用勾股定理求得QC的长,再求出AM,CM,利用等边三角形性质求出AP、PM、PC,由此即可解决问题.
解答  解:(Ⅰ)抛物线y=-x2-2x+3中,令y=-x2-2x+3=0,可得x1=1,x2=-3,
解:(Ⅰ)抛物线y=-x2-2x+3中,令y=-x2-2x+3=0,可得x1=1,x2=-3,
∴A(-3,0),C(1,0),
当x=0时,y=3,
∴B(0,3);
(Ⅱ)∵点D为AC中点,A(-3,0),C(1,0),
∴D(-1,0),
∵BE=2DE,B(0,3),
∴E(-$\frac{2}{3}$,1),
设直线CE为y=kx+b,把C(1,0),E(-$\frac{2}{3}$,1)代入,可得
$\left\{\begin{array}{l}{-\frac{2}{3}k+b=1}\\{k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{3}{5}}\\{b=\frac{3}{5}}\end{array}\right.$,
∴直线CE为y=-$\frac{3}{5}$x+$\frac{3}{5}$,
解方程组$\left\{\begin{array}{l}{y=-\frac{3}{5}x+\frac{3}{5}}\\{y=-{x}^{2}-2x+3}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{12}{5}}\\{y=\frac{51}{25}}\end{array}\right.$,
∵M在第二象限,
∴M(-$\frac{12}{5}$,$\frac{51}{25}$);
(Ⅲ)∵△APR和△AGQ是等边三角形,
∴AP=AR=PR,AQ=AG,∠QAG=∠RAP=60°,
∴∠QAR=∠GAP,
在△QAR和△GAP中,
$\left\{\begin{array}{l}{AQ=AG}\\{∠QAR=∠GAP}\\{AR=AP}\end{array}\right.$,
∴△QAR≌△GAP(SAS),
∴QR=PG,
∴PA+PC+PG=PR+PC+QR,
∴当Q,R,P,C共线时,PA+PC+PG的值最小,即为线段QC的长,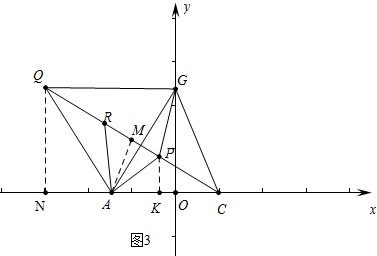
如图3,作QN⊥OA于N,作AM⊥CQ于M,作PK⊥CN于K,
依题意得∠GAO=45°+15°=60°,AO=3,
∴AG=GQ=QA=6,∠AGO=30°,OG=3$\sqrt{3}$,
∵∠AGQ=60°,
∴∠QGO=90°,
∴Q(-6,3$\sqrt{3}$),
在Rt△QNC中,QN=3$\sqrt{3}$,CN=6+1=7,
∴QC=$\sqrt{Q{N}^{2}+C{N}^{2}}$=2$\sqrt{19}$,即PA+PC+PG的最小值为2$\sqrt{19}$,
∴sin∠ACM=$\frac{AM}{AC}$=$\frac{QN}{QC}$,
∴AM=$\frac{AC•QN}{QC}$=$\frac{6\sqrt{57}}{19}$,
∵△APR是等边三角形,
∴∠APM=60°,PM=$\frac{\sqrt{3}}{3}$AM,MC=$\sqrt{A{C}^{2}-A{M}^{2}}$=$\frac{14\sqrt{19}}{19}$,
∴PC=CM-PM=$\frac{8\sqrt{19}}{19}$,
∵sin∠PCN=$\frac{PK}{PC}$=$\frac{QN}{QC}$,cos∠PCN=$\frac{CK}{CP}$=$\frac{CN}{CQ}$,
∴PK=$\frac{12\sqrt{3}}{19}$,CK=$\frac{28}{19}$,
∴OK=$\frac{9}{19}$,
∴P(-$\frac{9}{19}$,$\frac{12\sqrt{3}}{19}$).
点评 本题属于二次函数综合题,主要考查了等边三角形的性质、全等三角形的判定和性质、勾股定理以及解直角三角形等知识的综合应用,解题的关键是理解Q、R、P、C共线时,PA+PG+PC最小,学会添加常用辅助线,构造直角三角形,利用勾股定理计算求解.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
 已知二次函数y=-$\frac{1}{2}$x2-x+$\frac{3}{2}$.
已知二次函数y=-$\frac{1}{2}$x2-x+$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
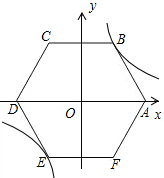 如图,在平面直角坐标系中,正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y=$\frac{9\sqrt{3}}{x}$位于第一象限的图象上,则正六边形ABCDEF的边长为6.
如图,在平面直角坐标系中,正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y=$\frac{9\sqrt{3}}{x}$位于第一象限的图象上,则正六边形ABCDEF的边长为6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 74.4127×1011元 | B. | 74.4127×1012元 | C. | 7.44127×1013元 | D. | 7.44127×1014元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),若想配一块与原来大小一样的三角形玻璃?应该带( )去.
小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),若想配一块与原来大小一样的三角形玻璃?应该带( )去.| A. | 第1块 | B. | 第2块 | C. | 第3块 | D. | 第4块 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com