
 ��ͼ����������A���ʾ��a��B���ʾ��b��C���ʾ��c����a��c����|a+3|+��c-7��2=0��
��ͼ����������A���ʾ��a��B���ʾ��b��C���ʾ��c����a��c����|a+3|+��c-7��2=0������ ��1�����÷Ǹ��������ʵ�a+3=0��c-7=0�����a��c��ֵ��
��2��������ԳƵ㣬���ɵó������
��3����b����С�����������ɵ�b=1�������������������ʾ��A��B��C�����ʾ�����������ɵ�AB��AC��BC�ij���
���� 2AB-BC=2��3t+4��-��6t+6����⼴�ɣ�
��� �⣺��1����|a+3|+��c-7��2=0��
��a+3=0��c-7=0��
��ã�a=-3��c=7��
�ʴ�Ϊ��-3��7��
��2�����������Ե�BΪ�۵����۵���ʹ��A����C��պ��غϣ����ۺ۴���ʾ����Ϊ2��
�ʴ�Ϊ��2��
��3����b��������������
��b=1��
��A���Ӧ�����֣�-3-5t��
B���Ӧ�����֣�1-2t��
C���Ӧ�����֣�7+4t��
AB=��1-2t��-��-3-5t��=3t+4��
AC=��7+4t��-��-3-5t��=9t+10��
BC=��7+4t��-��1-2t��=6t+6��
�ʴ�Ϊ��3t+4��9t+10��6t+6��
�ڲ��䣬
2AB-BC=2��3t+4��-��6t+6��=6t+8-6t-6=2��
���� ������Ҫ���������ἰ�����ľ��룬�Լ��Ǹ��������ʣ�����Ĺؼ�������������ص�����������ľ��룮


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
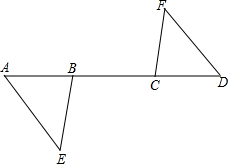 ��ͼ����֪��A��B��C��D��ͬһ��ֱ���ϣ�AC=BD����ABE=��DCF��BE=CF����֤����ABE�ա�DCF��
��ͼ����֪��A��B��C��D��ͬһ��ֱ���ϣ�AC=BD����ABE=��DCF��BE=CF����֤����ABE�ա�DCF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
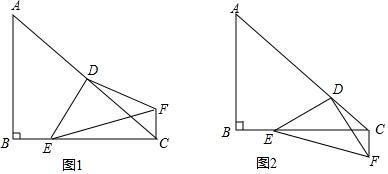
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com