
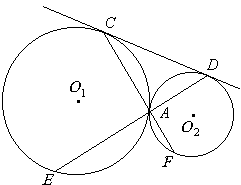
如图所示,⊙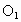 与⊙
与⊙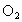 外切于A,CD为公切线,C、D为切点,延长CA交⊙
外切于A,CD为公切线,C、D为切点,延长CA交⊙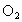 于F,延长DA交⊙
于F,延长DA交⊙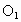 于E.求证:AC·AD=AE·AF.
于E.求证:AC·AD=AE·AF.
 53天天练系列答案
53天天练系列答案科目:初中数学 来源:黄冈重点作业 初三数学(下) 题型:044
如图所示,⊙O1与⊙O2外切于点O,以直线O1O2为x轴,点O为坐标原点,建立平面直角坐标系,直线AB切⊙O1于点B,切⊙O2于点A,交y轴于点C(0,2),交x轴于M,BO的延长线交⊙O2于D,且OB∶OD=1∶3.

(1)求⊙O2半径的长.
(2)求直线AB的解析式.
(3)在直线AB上是否存在点P,使△MO2P与△MOB相似?若存在,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:044
如图所示,⊙M与⊙N外切于点P,经过点P的直线AB交⊙M于A,交⊙N于点B,以⊙M为直径AC所在直线为y轴,经过点B的直线为x轴建立直角坐标系.
(1)求证OB是⊙N的切线;

(2)如果OC=CM=MA=1,⊙N在始终保持与⊙M外切,与比x轴相切的情况下运动,设点N的坐标为(x,y),求y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源:素质教育新学案·初中几何·第三册 题型:047
已知,如图所示,半圆![]() 与半圆
与半圆![]() 外切于点C,外公切线切半圆
外切于点C,外公切线切半圆![]() 于A,切半圆
于A,切半圆![]() 于B,BA延长线交
于B,BA延长线交![]() 的延长线于点P.
的延长线于点P.
(1)求证∠ACB=90°;
(2)求证![]() ;
;
(3)若![]() ,两圆半径之差为3,求以两圆半径为根的一元二次方程.
,两圆半径之差为3,求以两圆半径为根的一元二次方程.

查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
如图所示,⊙M与⊙N外切于点P.
经过点P的直线AB交⊙M于A,交⊙N于点B,以⊙M为直径AC所在直线为y轴,经过点B的直线为J轴建立直角坐标系.
(1)求证OB是⊙N的切线;

(2)如果OC=CM=MA=1,⊙N在始终保持与⊙M外切,与比x轴相切的情况下运动,设点N的坐标为(x,y),求y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源:中学学习一本通 数学 九年级下册 北师大课标 题型:047
如图所示,⊙O1与⊙O2外切于A,过点A的直线分别交⊙O1和⊙O2于点P,C.求证:PA∶PC=O1A∶O1O2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com