
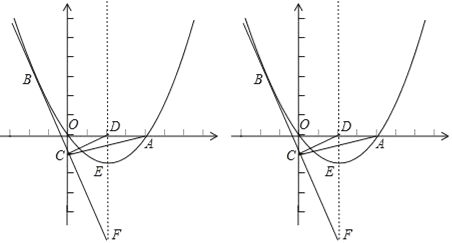
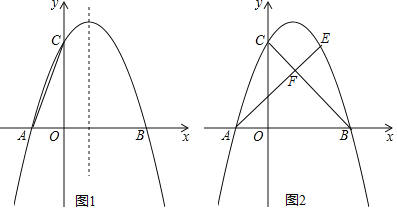
ЁОЬтФПЁПШчЭМЃЌвбжЊвбжЊХзЮяЯпОЙ§дЕуOКЭxжсЩЯвЛЕуAЃЈ4ЃЌ0ЃЉЃЌХзЮяЯпЖЅЕуЮЊEЃЌЫќЕФЖдГЦжсгыxжсНЛгкЕуDЃЌжБЯпy=Љ2xЉ1ОЙ§ХзЮяЯпЩЯвЛЕуBЃЈЉ2ЃЌmЃЉЧвгыyжсНЛгкЕуCЃЌгыХзЮяЯпЕФЖдГЦжсНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓmЕФжЕМАИУХзЮяЯпЕФНтЮіЪН
ЃЈ2ЃЉPЃЈxЃЌyЃЉЪЧХзЮяЯпЩЯЕФвЛЕуЃЌШєSЁїADP=SЁїADCЃЌЧѓГіЫљгаЗћКЯЬѕМўЕФЕуPЕФзјБъЃЎ
ЃЈ3ЃЉЕуQЪЧЦНУцФкШЮвтвЛЕуЃЌЕуMДгЕуFГіЗЂЃЌбиЖдГЦжсЯђЩЯвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШдШЫйдЫЖЏЃЌЩшЕуMЕФдЫЖЏЪБМфЮЊtУыЃЌЪЧЗёФмЪЙвдQЁЂAЁЂEЁЂMЫФЕуЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃПШєФмЃЌЧыжБНгаДГіЕуMЕФдЫЖЏЪБМфtЕФжЕЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1) 3 ![]() (2) P1ЃЈ2+2
(2) P1ЃЈ2+2![]() ЃЌ1ЃЉP2=ЃЈ2Љ2
ЃЌ1ЃЉP2=ЃЈ2Љ2![]() ЃЌ1ЃЉЃЌP3ЃЉ2ЃЌ1ЃЉ (3) Дцдк
ЃЌ1ЃЉЃЌP3ЃЉ2ЃЌ1ЃЉ (3) Дцдк
НтЃКЃЈ1ЃЉЁпЕуBЃЈЉ2ЃЌmЃЉдкжБЯпy=Љ2xЉ1ЩЯ
Ёрm=Љ2ЁСЃЈЉ2ЃЉЉ1=4Љ1=3ЃЌ
ЫљвдЃЌЕуBЃЈЉ2ЃЌ3ЃЉЃЌ
гжЁпХзЮяЯпОЙ§дЕуOЃЌ
ЁрЩшХзЮяЯпЕФНтЮіЪНЮЊy=ax2+bxЃЌ
ЁпЕуBЃЈЉ2ЃЌ3ЃЉЃЌAЃЈ4ЃЌ0ЃЉдкХзЮяЯпЩЯЃЌ
![]() ЃЌ
ЃЌ
НтЕУ ЃЎ
ЃЎ
ЁрХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЁпPЃЈxЃЌyЃЉЪЧХзЮяЯпЩЯЕФвЛЕуЃЌ
![]() ЃЌ
ЃЌ
ШєSЁїADP=SЁїADCЃЌ
![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
гжЁпЕуCЪЧжБЯпy=Љ2xЉ1гыyжсНЛЕуЃЌ
ЁрCЃЈ0ЃЌЉ1ЃЉЃЌ
ЁрOC=1ЃЌ
Ёр|![]() x2Љx|=1ЃЌМД
x2Љx|=1ЃЌМД![]() x2Љx=1ЃЌЛђ
x2Љx=1ЃЌЛђ![]() x2Љx=Љ1ЃЌ
x2Љx=Љ1ЃЌ
НтЕУЃКx1=2+2![]() ЃЌx2=2Љ2
ЃЌx2=2Љ2![]() ЃЌx3=x4=2ЃЌ
ЃЌx3=x4=2ЃЌ
ЁрЕуPЕФзјБъЮЊ P1ЃЈ2+2![]() ЃЌ1ЃЉP2=ЃЈ2Љ2
ЃЌ1ЃЉP2=ЃЈ2Љ2![]() ЃЌ1ЃЉЃЌP3ЃЉ2ЃЌ1ЃЉЃЛ
ЃЌ1ЃЉЃЌP3ЃЉ2ЃЌ1ЃЉЃЛ
ЃЈ3ЃЉНсТлЃКДцдкЃЎ
ЁпХзЮяЯпЕФНтЮіЪНЮЊy=![]() x2ЉxЃЌ
x2ЉxЃЌ
ЁрЖЅЕуEЃЈ2ЃЌЉ1ЃЉЃЌЖдГЦжсЮЊx=2ЃЛ
ЕуFЪЧжБЯпy=Љ2xЉ1гыЖдГЦжсx=2ЕФНЛЕуЃЌЁрFЃЈ2ЃЌЉ5ЃЉЃЌDF=5ЃЎ
гжЁпAЃЈ4ЃЌ0ЃЉЃЌ
ЁрAE=![]() ЃЎ
ЃЎ
ШчгвЭМЫљЪОЃЌдкЕуMЕФдЫЖЏЙ§ГЬжаЃЌвРДЮГіЯжЫФИіСтаЮЃК
ЂйСтаЮAEM1Q1ЃЎ
ЁпДЫЪБEM1=AE=![]() ЃЌ
ЃЌ
ЁрM1F=DFЉDEЉDM1=4Љ![]() ЃЌ
ЃЌ
Ёрt1=4Љ![]() ЃЛ
ЃЛ
ЂкСтаЮAEOM2ЃЎ
ЁпДЫЪБDM2=DE=1ЃЌ
ЁрM2F=DF+DM2=6ЃЌ
Ёрt2=6ЃЛ
ЂлСтаЮAEM3Q3ЃЎ
ЁпДЫЪБEM3=AE=![]() ЃЌ
ЃЌ
ЁрDM3=EM3ЉDE=![]() Љ1ЃЌ
Љ1ЃЌ
ЁрM3F=DM3+DF=ЃЈ![]() Љ1ЃЉ+5=4+
Љ1ЃЉ+5=4+![]() ЃЌ
ЃЌ
Ёрt3=4+![]() ЃЛ
ЃЛ
ЂмСтаЮAM4EQ4ЃЎ
ДЫЪБAEЮЊСтаЮЕФЖдНЧЯпЃЌЩшЖдНЧЯпAEгыM4Q4НЛгкЕуHЃЌдђAEЁЭM4Q4ЃЌ
ЁпвзжЊЁїAEDЁзЁїM4EHЃЌ
![]() ЃЌМД
ЃЌМД ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
ЁрDM4=M4EЉDE=![]() Љ1=
Љ1=![]() ЃЌ
ЃЌ
ЁрM4F=DM4+DF=![]() +5=
+5=![]() ЃЌ
ЃЌ
Ёрt4=![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌДцдкЕуMЁЂЕуQЃЌЪЙЕУвдQЁЂAЁЂEЁЂMЫФЕуЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃЛЪБМфtЕФжЕЮЊЃКt1=4Љ![]() ЃЌt2=6ЃЌt3=4+
ЃЌt2=6ЃЌt3=4+![]() ЃЌt4=
ЃЌt4=![]() ЃЎ
ЃЎ
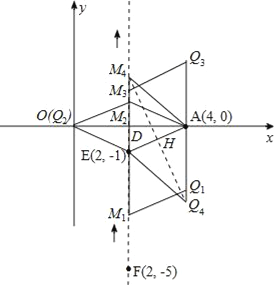
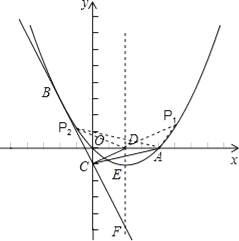
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉНЋx=-2ДњШыy=-2x-1МДПЩЧѓЕУЕуBЕФзјБъЃЌИљОнХзЮяЯпЙ§ЕуAЁЂOЁЂBМДПЩЧѓГіХзЮяЯпЕФЗНГЬ.
ЃЈ2ЃЉИљОнЬтвтЃЌПЩжЊЁїADPКЭЁїADCЕФИпЯрЕШЃЌМДЕуPзнзјБъЕФОјЖджЕЮЊ1ЃЌЫљвдЕуPЕФзнзјБъЮЊ![]() ЃЌЗжБ№ДњШы
ЃЌЗжБ№ДњШы![]() жаЧѓНтЃЌМДПЩЕУЕНЫљгаЗћКЯЬтвтЕФЕуPЕФзјБъЁЃ
жаЧѓНтЃЌМДПЩЕУЕНЫљгаЗћКЯЬтвтЕФЕуPЕФзјБъЁЃ
ЃЈ3ЃЉгЩХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌЕУЖЅЕуEЃЈ2ЃЌЉ1ЃЉЃЌЖдГЦжсЮЊx=2ЃЛ
ЃЌЕУЖЅЕуEЃЈ2ЃЌЉ1ЃЉЃЌЖдГЦжсЮЊx=2ЃЛ
ЕуFЪЧжБЯпy=Љ2xЉ1гыЖдГЦжсx=2ЕФНЛЕуЃЌЧѓГіFЃЈ2ЃЌЉ5ЃЉЃЌDF=5ЃЎ
гжгЩAЃЈ4ЃЌ0ЃЉЃЌИљОнЙДЙЩЖЈРэЕУ![]() ЃЎШЛКѓЗж4жжЧщПіЧѓНт.
ЃЎШЛКѓЗж4жжЧщПіЧѓНт.


 УћЬтбЕСЗЯЕСаД№АИ
УћЬтбЕСЗЯЕСаД№АИ ЦкФЉМЏНсКХЯЕСаД№АИ
ЦкФЉМЏНсКХЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
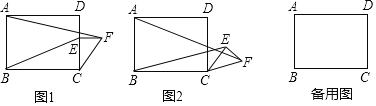
ЁОЬтФПЁПШчЭМ1ЃЌдкОиаЮABCDжаЃЌABЃН6ЃЌBCЃН8ЃЌЕуEЪЧБпCDЩЯЕФЕуЃЌЧвCEЃН4ЃЌЙ§ЕуEзїCDЕФДЙЯпЃЌВЂдкДЙЯпЩЯНиШЁEFЃН3ЃЌСЌНгCFЃЎНЋЁїCEFШЦЕуCАДЫГЪБеыЗНЯђа§зЊЃЌМЧа§зЊНЧЮЊaЃЎ
ЃЈ1ЃЉЮЪЬтЗЂЯж
ЕБaЃН0ЁуЪБЃЌAFЃНЁЁ ЃЌBEЃНЁЁ ЃЌ![]() ЃНЁЁ ЃЛ
ЃНЁЁ ЃЛ
ЃЈ2ЃЉЭиеЙЬНОП
ЪдХаЖЯЃКЕБ0ЁуЁмaЁуЃМ360ЁуЪБЃЌ![]() ЕФДѓаЁгаЮоБфЛЏЃПЧыНіОЭЭМ2ЕФЧщПіИјГіжЄУїЃЎ
ЕФДѓаЁгаЮоБфЛЏЃПЧыНіОЭЭМ2ЕФЧщПіИјГіжЄУїЃЎ
ЃЈ3ЃЉЮЪЬтНтОі
ЕБЁїCEFа§зЊжСAЃЌEЃЌFШ§ЕуЙВЯпЪБЃЌжБНгаДГіЯпЖЮBEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
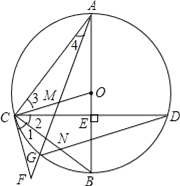
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЕуCдкABЕФбгГЄЯпЩЯЃЌADЦНЗжЁЯCAEНЛЁбOгкЕуDЃЌЧвAEЁЭCDЃЌДЙзуЮЊЕуEЃЎ
ЃЈ1ЃЉЧѓжЄЃКжБЯпCEЪЧЁбOЕФЧаЯпЃЎ
ЃЈ2ЃЉШєBC=3ЃЌCD=3![]() ЃЌЧѓЯвADЕФГЄЃЎ
ЃЌЧѓЯвADЕФГЄЃЎ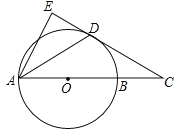
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+4гыxжсНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЁЂBЃЈ3ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌDЮЊХзЮяЯпЖдГЦжсЩЯвЛЖЏЕуЃЌЧѓDдЫЖЏЕНЪВУДЮЛжУЪБЁїDACЕФжмГЄзюаЁЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕуEдкЕквЛЯѓЯоХзЮяЯпЩЯЃЌAEгыBCНЛгкЕуFЃЌШєAFЃКFEЃН2ЃК1ЃЌЧѓEЕузјБъЃЛ
ЃЈ4ЃЉЕуMЁЂNЭЌЪБДгBЕуГіЗЂЃЌЗжБ№биBAЁЂBCЗНЯђдЫЖЏЃЌЫќУЧЕФдЫЖЏЫйЖШЖМЪЧ1ИіЕЅЮЛ/УыЃЌЕБЕуMдЫЖЏЕНЕуAЪБЃЌЕуNЭЃжЙдЫЖЏЃЌдђЕБЕуNЭЃжЙдЫЖЏКѓЃЌдкxжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУЁїPBNЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌжБНгаДГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
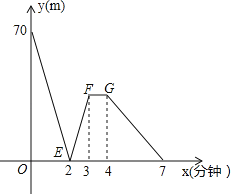
ЁОЬтФПЁПгавЛПЦММаЁзщНјааСЫЛњЦїШЫаазпадФмЪдбщЃЎдкЪдбщГЁЕигаAЁЂBЁЂCШ§ЕуЫГДЮдкЭЌвЛБЪжБЕФШќЕРЩЯЃЌМзЁЂввСНЛњЦїШЫЗжБ№ДгAЁЂBСНЕуЭЌЪБЭЌЯђГіЗЂЃЌОЙ§7minЭЌЪБЕНДяCЕуЃЌввЛњЦїШЫЪМжевд60m/minЕФЫйЖШаазпЃЌШчЭМЪЧМзЁЂввСНЛњЦїШЫжЎМфЕФОрРыyЃЈmЃЉгыЫћУЧЕФаазпЪБМфxЃЈminЃЉжЎМфЕФКЏЪ§ЭМЯѓЃЌЧыНсКЯЭМЯѓЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉAЁЂBСНЕужЎМфЕФОрРыЪЧЁЁ ЁЁЃЎmЃЌМзЛњЦїШЫЧА2minЕФЫйЖШЮЊЁЁ ЁЁЃЎm/minЃЛ
ЃЈ2ЃЉШєЧА3minМзЛњЦїШЫЕФЫйЖШВЛБфЃЌЧѓЯпЖЮEFЫљдкжБЯпЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉжБНгаДГіСНЛњЦїШЫГіЗЂЖрГЄЪБМфЯрОр28mЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
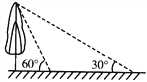
ЁОЬтФПЁПШчЭМЃЌаЃдАФкгавЛПУгыЕиУцДЙжБЕФЪїЃЌЪ§бЇаЫШЄаЁзщСНДЮВтСПЫќдкЕиУцЩЯЕФгАзгЃЌЕквЛДЮЪЧбєЙтгыЕиУцГЩ60ЁуНЧЪБЃЌЕкЖўДЮЪЧбєЙтгыЕиУцГЩ30ЁуНЧЪБЃЌСНДЮВтСПЕФгАГЄЯрВю8УзЃЌдђЪїИп_____________Уз(НсЙћБЃСєИљКХ)ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
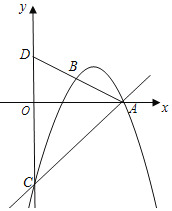
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+4x+cЙ§ЕуA(6ЃЌ0)ЁЂB(3ЃЌ![]() )ЃЌгыyжсНЛгкЕуCЃЎСЊНсABВЂбгГЄЃЌНЛyжсгкЕуDЃЎ
)ЃЌгыyжсНЛгкЕуCЃЎСЊНсABВЂбгГЄЃЌНЛyжсгкЕуDЃЎ
(1)ЧѓИУХзЮяЯпЕФБэДяЪНЃЛ
(2)ЧѓЁїADCЕФУцЛ§ЃЛ
(3)ЕуPдкЯпЖЮACЩЯЃЌШчЙћЁїOAPКЭЁїDCAЯрЫЦЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћвЛИіШ§НЧаЮгавЛЬѕБпЩЯЕФИпЕШгкетЬѕБпЕФвЛАыЃЌФЧУДЮвУЧАбетИіШ§НЧаЮНазіЁААыИпШ§НЧаЮЁБЃЎ
ШчЭМ1ЃЌЖдгкЁїABCЃЌBCБпЩЯЕФИпADЕШгкBCЕФвЛАыЃЌЁїABCОЭЪЧАыИпШ§НЧаЮЃЌДЫЪБЃЌГЦЁїABCЪЧBCРрАыИпШ§НЧаЮЃЛШчЭМ2ЃЌЖдгкЁїEFGЃЌEFБпЩЯЕФИпGHЕШгкEFЕФвЛАыЃЌЁїEFGОЭЪЧАыИпШ§НЧаЮЃЌДЫЪБЃЌГЦЁїEFGЪЧEFРрАыИпШ§НЧаЮЃЎ
ЃЈ1ЃЉжБНгаДГіЯТСа3ИіаЁЬтЕФД№АИЃЎ
ЂйШєвЛИіШ§НЧаЮМШЪЧЕШбќШ§НЧаЮгжЪЧАыИпШ§НЧаЮЃЌдђЦфЕзНЧЖШЪ§ЕФЫљгаПЩФмжЕЮЊЁЁ ЃЎ
ЂкШєвЛИіШ§НЧаЮМШЪЧжБНЧШ§НЧаЮгжЪЧАыИпШ§НЧаЮЃЌдђЦфзюаЁНЧЕФе§ЧажЕЮЊЁЁ ЃЎ
ЂлШчЭМ3ЃЌе§ЗНаЮЭјИёжаЃЌLЃЌMЪЧвбжЊЕФСНИіИёЕуЃЌШєИёЕуNЪЙЕУЁїLMNЮЊАыИпШ§НЧаЮЃЌЧвЁїLMNЮЊЕШбќШ§НЧаЮЛђжБНЧШ§НЧаЮЃЌдђетбљЕФИёЕуNЙВгаЁЁ ИіЃЎ
ЃЈ2ЃЉШчЭМЃЌЦНУцжБНЧзјБъЯЕФкЃЌжБЯпyЃНx+2гыХзЮяЯпyЃНx2НЛгкRЃЌSСНЕуЃЌЕуTзјБъЮЊЃЈ0ЃЌ5ЃЉЃЌЕуPЪЧХзЮяЯпyЃНx2ЩЯЕФвЛИіЖЏЕуЃЌЕуQЪЧзјБъЯЕФквЛЕуЃЌЧвЪЙЕУЁїRSQЮЊRSРрАыИпШ§НЧаЮЃЎ
ЂйЕБЕуPНщгкЕуRгыЕуSжЎМфЃЈАќРЈЕуRЃЌSЃЉЃЌЧвPQШЁЕУзюаЁжЕЪБЃЌЧѓЕуPЕФзјБъЃЎ
ЂкЕБЕуPНщгкЕуRгыЕуOжЎМфЃЈАќРЈЕуRЃЌOЃЉЪБЃЌЧѓPQ+![]() QTЕФзюаЁжЕЃЎ
QTЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаЛЊЮФУїЃЌдДдЖСїГЄЃЛжаЛЊККзжЃЌдЂвтЩюЙуЃЎЮЊСЫДЋГажаЛЊУёзхгХауДЋЭГЮФЛЏЃЌЮвЪаФГжабЇОйааЁАККзжЬ§аДЁББШШќЃЌШќКѓећРэВЮШќбЇЩњЕФГЩМЈЃЌНЋбЇЩњЕФГЩМЈЗжЮЊAЃЌBЃЌCЃЌDЫФИіЕШМЖЃЌВЂНЋНсЙћЛцжЦГЩШчЭМЫљЪОЕФЬѕаЮЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЌЕЋОљВЛЭъећЃЎ

ЧыФуИљОнЭГМЦЭМНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉВЮМгБШШќЕФбЇЩњЙВга____УћЃЛ
ЃЈ2ЃЉдкЩШаЮЭГМЦЭМжаЃЌmЕФжЕЮЊ____ЃЌБэЪОЁАDЕШМЖЁБЕФЩШаЮЕФдВаФНЧЮЊ____ЖШЃЛ
ЃЈ3ЃЉзщЮЏЛсОіЖЈДгБОДЮБШШќЛёЕУAЕШМЖЕФбЇЩњжаЃЌбЁГі2УћШЅВЮМгШЋЪажабЇЩњЁАККзжЬ§аДЁБДѓШќЃЎвбжЊAЕШМЖбЇЩњжаФаЩњга1УћЃЌЧыгУСаБэЗЈЛђЛЪїзДЭМЗЈЧѓГіЫљбЁ2УћбЇЩњЧЁКУЪЧвЛУћФаЩњКЭвЛУћХЎЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com