
【题目】如图,在![]() ,
,![]() ,以
,以![]() 为圆心,任意长为半径画弧,分别交
为圆心,任意长为半径画弧,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,再分别以
,再分别以![]() ,
,![]() ,为圆心,大于
,为圆心,大于![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ,作弧线
,作弧线![]() ,交
,交![]() 于点
于点![]() .已知
.已知![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.

(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() .①以点
.①以点![]() 为圆心,
为圆心,![]() 长为半径画弧,分别交
长为半径画弧,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ;②在分别以
;②在分别以![]() 、
、![]() 为圆心,
为圆心,![]() 长为半径画弧,两弧交于点
长为半径画弧,两弧交于点![]() ;③连结
;③连结![]() 、
、![]() ,则四边形
,则四边形![]() 的面积为( )
的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
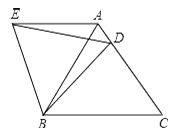
【题目】在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列四个结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△AED的周长是9.其中正确的结论是__(把你认为正确结论的序号都填上.)
查看答案和解析>>
科目:初中数学 来源: 题型:
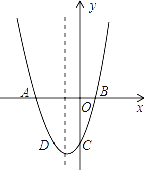
【题目】(12分)已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有A、B两种型号台灯,若购买2台A型台灯和6台B型台灯共需610元.若购买6台A型台灯和2台B型台灯共需470元.
(1)求A、B两种型号台灯每台分别多少元?
(2)采购员小红想采购A、B两种型号台灯共30台,且总费用不超过2200元,则最多能采购B型台灯多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个边长为m+3的正方形,先将这个正方形两邻边长分别增加1和减少1,得到的长方形①的面积为S1.
(1)试探究该正方形的面积S与S1的差是否是一个常数,如果是,求出这个常数;如果不是,说明理由;
(2)再将这个正方形两邻边长分别增加4和减少2,得到的长方形②的面积为S2.
①试比较S1,S2的大小;
②当m为正整数时,若某个图形的面积介于S1,S2之间(不包括S1,S2)且面积为整数,这样的整数值有且只有16个,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海中两个灯塔A,B,其中B位于A的正东方向上,渔船跟踪鱼群由西向东航行,在点C处测得灯塔A在西北方向上,灯塔B在北偏东30°方向上,渔船不改变航向继续向东航行30海里到达点D,这时测得灯塔A在北偏西60°方向上,求灯塔A,B间的距离.(计算结果用根号表示,不取近似值)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com