
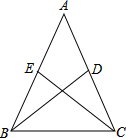
 已知:如图,在△ABC中,AB=AC,BD,CE是△ABC的中线.
已知:如图,在△ABC中,AB=AC,BD,CE是△ABC的中线.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
|


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
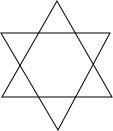 某村建造农民文化公园,将12个场馆排成6行,每行4个场馆.村委会将如图的设计方案公布后,引起一群初中生的好奇,他们纷纷设计出不少精美对称的图案,请你也试试把12个场馆设计成符合要求的轴对称图形.
某村建造农民文化公园,将12个场馆排成6行,每行4个场馆.村委会将如图的设计方案公布后,引起一群初中生的好奇,他们纷纷设计出不少精美对称的图案,请你也试试把12个场馆设计成符合要求的轴对称图形.查看答案和解析>>
科目:初中数学 来源: 题型:
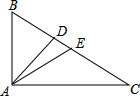 如图,在△ABC中,∠BAC=90°,AB=3cm,AC=4cm,AD是高线,AE是中线.
如图,在△ABC中,∠BAC=90°,AB=3cm,AC=4cm,AD是高线,AE是中线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com