
【题目】如图,在△ABC中,AD为∠BAC的平分线,BM⊥AD,垂足为M,且AB=5,BM=2,AC=9,则∠ABC与∠C的关系为( )

A.∠ABC=2∠CB.∠ABC=![]() ∠CC.
∠CC.![]() ∠ABC=∠CD.∠ABC=3∠C
∠ABC=∠CD.∠ABC=3∠C
 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( )

A.内部 B.外部 C.边上 D.以上都有可能
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2﹣4x+3与x轴交于A,B两点,其顶点为C.
(1)对于任意实数m,点M(m,﹣2)是否在该抛物线上?请说明理由;
(2)求证:△ABC是等腰直角三角形;
(3)若点D在x轴上,则在抛物线上是否存在点P,使得PD∥BC,且PD=BC?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.2万元,乙队每天的施工费用为5.8万元.工程预算的施工费用为501万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,CF平分∠DCE,若∠DCF=30°,∠E=20°,求∠ABE的度数.
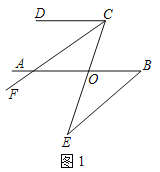
(2)如图2,已知AB∥CD,CF平分∠DCE,∠EBF=2∠ABF,若∠F的2倍与∠E的补角的和为190°,求∠ABE的度数.
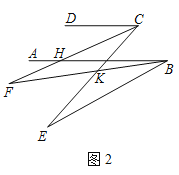
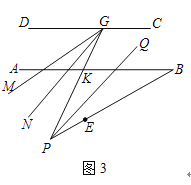
(3)如图3,若P是(2)中的射线BE上一点,G是CD上任一点,PQ∥GN,PQ平分∠BPG,GM平分∠DGP,若∠B=30°,求∠MGN的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,AB=AC=20cm,BD⊥AC于D,且BD=16cm.点M从点A出发,沿AC方向匀速运动,速度为4cm/s;同时点P由B点出发,沿BA方向匀速运动,速度为lcm/s,过点P的动直线PQ∥AC,交BC于点Q,连结PM,设运动时间为t(s)(0<t<5),解答下列问题:
(1)线段AD=___cm;
(2)求证:PB=PQ;
(3)当t为何值时,以P、Q、D、M为顶点的四边形为平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯,荣获了诺贝尔物理学奖.石墨烯目前是世上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在△ABC中,∠C=60°,∠A=40°.

(1)用尺规作图作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com