Question

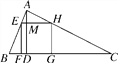
【题目】如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFGH的一边FG在BC上，顶点E，H分别在AB，AC上，已知BC＝40cm，AD＝30cm.

（1）求证：△AEH∽△ABC；

（2）求这个正方形的边长与面积.

Answer 1

【答案】（1）详见解析；（2）正方形EFGH的边长为cm，面积为 cm2.

【解析】试题分析：（1）由正方形可得EH∥BC，所以可以得到对应的两组角相等，即可证明相似；（2）设正方形边长为x，再由△AEH∽△ABC得到对应边成比例，列出关于x的方程，解出x即可．

试题解析：

(1)证明：∵四边形EFGH是正方形，∴EH∥BC，∴∠AEH＝∠B，∠AHE＝∠C，∴△AEH∽△ABC；

(2)解：∵∠EFD＝∠FEM＝∠FDM＝90°，∴四边形EFDM是矩形，∴EF＝DM.设正方形EFGH的边长为xcm，∵△AEH∽△ABC，∴ ，∴，解得x＝.

∴正方形EFGH的边长为cm，面积为 cm2.

点睛:两个三角形的相似比等于对应的高之比,角平分线之比,中线之比．